题目内容
已知椭圆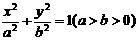 的左右焦点分别为
的左右焦点分别为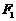 、
、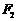 ,短轴两个端点为
,短轴两个端点为 、
、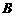 ,且四边形
,且四边形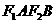 是边长为2的正方形.
是边长为2的正方形.
(I)求椭圆方程;
(Ⅱ)若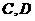 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点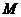 满足
满足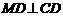 ,连接
,连接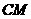 ,交椭圆于点
,交椭圆于点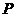 ,证明:
,证明: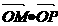 为定值;
为定值;
(III)在(Ⅱ)的条件下,试问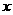 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点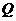 ,使得以
,使得以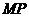 为直径的圆恒过直线
为直径的圆恒过直线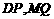 的交点?若存在,求出点Q的坐标;若不存在,请说明理由.
的交点?若存在,求出点Q的坐标;若不存在,请说明理由.
解:(I) ,
, ,
, 椭圆方程为
椭圆方程为 ,………4分
,………4分
(Ⅱ) ,设
,设 ,则
,则 ,
,
直线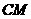 :
: ,即
,即 ,
,
代入椭圆 得
得 ,
,
 ,
, ,
, ,
,

 (定值),………10分
(定值),………10分
(III)设存在 满足条件,则
满足条件,则 ,
,

则由 =0得
=0得 ,从而得m=0
,从而得m=0
∴存在Q(0,0)满足条件

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
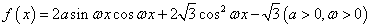 的最大值为2,且最小正周期为
的最大值为2,且最小正周期为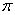 .
.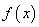 的解析式及其对称轴方程;
的解析式及其对称轴方程;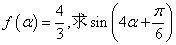 的值.
的值.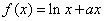 存在与直线
存在与直线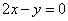 平行的切线,则实数
平行的切线,则实数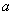 的取值范围
的取值范围 的虚部是__ ___.
的虚部是__ ___. .
. 的最大值,并写出
的最大值,并写出 中,角
中,角 的对边分别为
的对边分别为 若
若
 求实数
求实数 的最小值.
的最小值. , 则①处应填( )
, 则①处应填( )
 的方程
的方程 恒有实数解,则实数
恒有实数解,则实数 的取值范围是( )
的取值范围是( ) B.
B.  C.
C.  D.
D. 
 ,且
,且 在区间
在区间 有最小
有最小 值为( )
值为( ) B.
B.  C.
C.  D.
D. 