题目内容
已知1+i是实系数方程x2+ax+b=0的一个根．
（1）求a，b的值；
（2）试判断1-i是否是方程的根．
（1）求a，b的值；
（2）试判断1-i是否是方程的根．
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：（1）依题意，将1+i代入方程x2+ax+b=0，利用两复数相等即可求得a、b的值；
（2）把1-i代入方程左端，可结果是否为0即可．
（2）把1-i代入方程左端，可结果是否为0即可．
解答：
解：（1）∵1+i是方程x2+ax+b=0的根，
∴（1+i）2+a（1+i）+b=0，
即（a+b）+（a+2）i=0．
∴
，解得
．
∴a，b的值为a=-2，b=2．
（2）方程为x2-2x+2=0，
把1-i代入方程，
左边=（1-i）2-2（1-i）+2=-2i-2+2i+2=0，显然方程成立．
∴1-i也是方程的一个根．
∴（1+i）2+a（1+i）+b=0，
即（a+b）+（a+2）i=0．
∴
|
|
∴a，b的值为a=-2，b=2．
（2）方程为x2-2x+2=0，
把1-i代入方程，
左边=（1-i）2-2（1-i）+2=-2i-2+2i+2=0，显然方程成立．
∴1-i也是方程的一个根．
点评：本题考查复数代数形式的混合运算，突出考查复数相等的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
某班2013年元旦联欢会原定的9个歌唱节目已排成节目单，但在开演前又增加了两个新节目，如果将这两个节目插入原节目单中，那么不同插法的种数为（ ）
| A、110 | B、120 |
| C、20 | D、12 |
如图，在山底测得山顶仰角∠CAB=45°，沿倾斜角为30°的斜坡走1000米至S点，又测得山顶仰角为75°，求山高BC．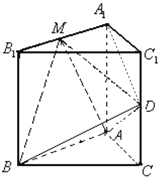
（文）如图，在直三棱柱ABC-A1B1C1中，AB⊥AC，AA1=AB=AC=1，∠ABC=