题目内容
12．设数列{an}的前n项和Sn满足Sn=2an-a1，且a3，a2+1，a1成等差数列．（1）求数列{an}的通项公式；
（2）设bn=$\frac{1}{{a}_{n}}$+2n，求数列{bn}的前n项和Tn．
分析 （1）由数列{an}的前n项和Sn满足Sn=2an-a1，分别取n=1，2，3，可得：a2=2a1，a3=4a1．由a3，a2+1，a1成等差数列．可得2（a2+1）=a1+a3，解得a1=2．再利用递推关系、等比数列的通项公式即可得出．
（2）bn=$\frac{1}{{a}_{n}}$+2n=$\frac{1}{{2}^{n}}$+2n，利用等差数列与等比数列的前n项和公式即可得出．
解答 解：（1）∵数列{an}的前n项和Sn满足Sn=2an-a1，∴a1=2a1-a1，a1+a2=2a2-a1，a1+a2+a3=2a3-a1，
解得a2=2a1，a3=4a1．
∵a3，a2+1，a1成等差数列．
∴2（a2+1）=a1+a3，
∴2（2a1+1）=a1+4a1，解得a1=2．
当n≥2时，an=Sn-Sn-1=2an-a1-（2an-1-a1），化为：an=2an-1．
∴数列{an}是等比数列，首项为2，公比为2．
∴an=2×2n-1=2n．
（2）bn=$\frac{1}{{a}_{n}}$+2n=$\frac{1}{{2}^{n}}$+2n，
∴数列{bn}的前n项和Tn=$（\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n}}）$+2（1+2+…+n）
=$\frac{\frac{1}{2}（1-\frac{1}{{2}^{n}}）}{1-\frac{1}{2}}$+2×$\frac{n（1+n）}{2}$
=$1-\frac{1}{{2}^{n}}$+n+n2．
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、递推关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
3．如图，正方体ABCD-A1B1C1D1中，棱长为1，点P在体对角线上，PB=$\frac{1}{3}$PB′，则P点坐标为（ ）
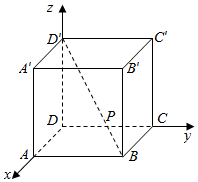
| A． | （$\frac{1}{3}$$，\frac{1}{3}$，$\frac{1}{3}$） | B． | （$\frac{2}{3}$，$\frac{2}{3}$，$\frac{2}{3}$） | C． | （$\frac{5}{6}$，$\frac{5}{6}$，$\frac{1}{6}$） | D． | （$\frac{2}{3}$，$\frac{2}{3}$，$\frac{1}{3}$） |
如图，在四棱锥P-ABCD中，E，F，G分别是PB，AB，PC的中点，若四边形ABCD是平行四边形．求证：平面EFG∥平面PAD．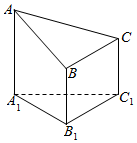
如图是一个以△A1B1C1为底面的直角三棱柱被一平面截得的几何体，截面为△ABC，已知AA1=4，BB1=2，CC1=3，在边AB上是否存在一点O，使得OC∥平面A1B1C1？