题目内容
7.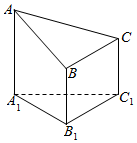 如图是一个以△A1B1C1为底面的直角三棱柱被一平面截得的几何体,截面为△ABC,已知AA1=4,BB1=2,CC1=3,在边AB上是否存在一点O,使得OC∥平面A1B1C1?
如图是一个以△A1B1C1为底面的直角三棱柱被一平面截得的几何体,截面为△ABC,已知AA1=4,BB1=2,CC1=3,在边AB上是否存在一点O,使得OC∥平面A1B1C1?
分析 作OD∥AA1交A1B1于D,连C1D,根据梯形中位线定理及平行四边形判定定理,可得四边形ODC1C是平行四边形,进而OC∥C1D,根据线面平行的判定定理,可得OC∥平面A1B1C1.
解答  证明:在边AB上存在AB的中点O,使得OC∥平面A1B1C1.
证明:在边AB上存在AB的中点O,使得OC∥平面A1B1C1.
取AB的中点O,作OD∥AA1交A1B1于D,连C1D,
则OD∥BB1∥CC1,
因为O是AB的中点,
所以OD=$\frac{1}{2}$(AA1+BB1)=3=CC1,
则四边形ODC1C是平行四边形,
因此有OC∥C1D,C1D?平面C1B1A1,
且OC?平面C1B1A1,
则OC∥平面A1B1C1.
点评 本题主要考查了直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
5.已知集合A={x|x=2k+1,k∈Z},集合B={x|x=4k±1,k∈Z},则( )
| A. | A⊆B | B. | A?B | C. | A=B | D. | B⊆A |
15.已知a<-1<b<0<c<1,则下列不等式成立的是( )
| A. | b2<c<a2 | B. | ab+$\frac{1}{ab}$<c | C. | $\frac{1}{b}$<$\frac{1}{a}$<$\frac{1}{c}$ | D. | b2>ab-bc+ac |
16.已知x,y满足$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,若不等式ax-y≥1恒成立,则实数a的取值范围是( )
| A. | $[{\frac{27}{5},+∞})$ | B. | $[{\frac{11}{5},+∞})$ | C. | $[{\frac{3}{5},+∞})$ | D. | [2,+∞) |
17.已知cos$({\frac{π}{2}+α})$=$\frac{1}{3}$,则1-cos2α的值为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{9}$ |
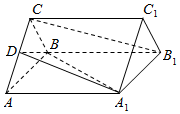 如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.