题目内容
1.已知函数f(x)=$\frac{4}{|x|+2}$-1的定义域是[a,b](a,b为整数),值域是[0,1],请在后面的下划线上写出所有满足条件的整数数对(a,b)(-2,0),(-2,1),(-2,2),(-1,2),(0,2).分析 根据函数的值域先求出满足条件的条件x,结合函数的定义域进行求解即可.
解答  解:由f(x)=$\frac{4}{|x|+2}$-1=0得$\frac{4}{|x|+2}$=1,得|x|+2=4,即|x|=2,得x=2或-2,
解:由f(x)=$\frac{4}{|x|+2}$-1=0得$\frac{4}{|x|+2}$=1,得|x|+2=4,即|x|=2,得x=2或-2,
由f(x)=$\frac{4}{|x|+2}$-1=1得$\frac{4}{|x|+2}$=2,得|x|+2=2,即|x|=0,得x=0,
则定义域为可能为[-2,0],[-2,1],[-2,2],[-1,2],[0,2],
则满足条件的整数数对(a,b)为(-2,0),(-2,1),(-2,2),(-1,2),(0,2),
故答案为:(-2,0),(-2,1),(-2,2),(-1,2),(0,2),
点评 本题主要考查函数定义域和值域的应用,根据条件求出函数值对应的x是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知x,y满足$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,若不等式ax-y≥1恒成立,则实数a的取值范围是( )
| A. | $[{\frac{27}{5},+∞})$ | B. | $[{\frac{11}{5},+∞})$ | C. | $[{\frac{3}{5},+∞})$ | D. | [2,+∞) |
10.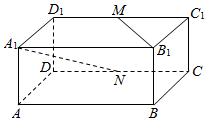 长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
 长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | 0 | C. | $\frac{\sqrt{15}}{10}$ | D. | $\frac{1}{6}$ |
11.若集合A={x|-x2+2x≤0},B={x|x>1},则A∪B等于( )
| A. | [2,+∞) | B. | [0,+∞) | C. | (1,2] | D. | (-∞,0]∪(1,+∞) |
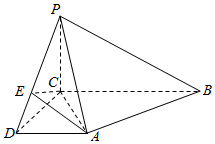 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.