题目内容
18．已知函数f（x）=ax3-2x的图象过点P（-1，4），则曲线y=f（x）在点P处的切线方程为8x+y+4=0．分析 将P的坐标代入f（x），可得a的值，求出f（x）的导数，可得切线的斜率，运用点斜式方程可得切线的方程．
解答 解：函数f（x）=ax3-2x的图象过点P（-1，4），
可得-a+2=4，解得a=-2，
则f（x）=-2x3-2x，
f（x）的导数为f′（x）=-6x2-2，
则曲线y=f（x）在点P处的切线斜率为-8，
可得曲线y=f（x）在点P处的切线方程为y-4=-8（x+1），
即为8x+y+4=0．
故答案为：8x+y+4=0．
点评 本题考查导数的运用：求切线方程，考查导数的几何意义，正确求导和运用点斜式方程是解题的关键，属于基础题．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
6．运行如图所示的程序框图，若输出的S是510，则①应为（ ）
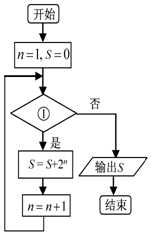
| A． | n≤5 | B． | n≤6 | C． | n≤7 | D． | n≤8 |
13．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°，且|$\overrightarrow{a}$|=$\sqrt{3}$，|$\overrightarrow{b}$|=2，则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于（ ）
| A． | 1 | B． | $\sqrt{13}$ | C． | 13 | D． | $\sqrt{7-2\sqrt{3}}$ |
12．连掷两次骰子分别得到点数m，n，则向量（m，n与向量（-1，1）的夹角θ＞90°的概率是（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{7}{12}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
9．对任意的实数R，集合A={x|x2+x-6＞0}，B={-1，0，1，2，3，4}．则B∩∁RA=（ ）
| A． | {2，3，4，5} | B． | {-1，0} | C． | {-1，0，1，2} | D． | { 2，3，4} |