题目内容
已知下面各数列{an}的前n项和Sn的公式,且 Sn=3n-2.则数列{an}的通项公式是 .
考点:数列递推式
专题:等差数列与等比数列
分析:由已知条件,利用公式an=
能求出结果.
|
解答:
解:∵Sn=3n-2,
∴n=1时,a1=S1=3-2=1,
n≥2时,an=Sn-Sn-1=(3n-2)-(3n-1)+2=
•3n,
∴an=
.
故答案为:an=
.
∴n=1时,a1=S1=3-2=1,
n≥2时,an=Sn-Sn-1=(3n-2)-(3n-1)+2=
| 2 |
| 3 |
∴an=
|
故答案为:an=
|
点评:本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意公式an=
的合理运用.
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
轮船A和轮船B在某日中午12时离开海港C,两艘轮船的航行方向之间的夹角为120°,轮船A的航行速度是25/h,轮船B的航行速度是15n mile/h,则该日下午2时A、B两船之间的距离是( )
| A、35 n mile | ||
B、5
| ||
| C、70 n mile | ||
D、10
|
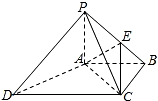 四棱锥P-ABCD中,DC∥AB,AB=2DC=4
四棱锥P-ABCD中,DC∥AB,AB=2DC=4 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=2AB=2,E是线段PD上的点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=2AB=2,E是线段PD上的点.