题目内容
9.下列命题中正确的个数是( )①命题“?x∈(1,+∞),2x>2”的否定是“?x∉(1,+∞),2x>2”;
②“a=2”是“|a|=2”的必要不充分条件;
③若命题p为真,命题¬q为真,则命题p∧q为真;
④命题“在△ABC中,若$sinA<\frac{1}{2}$,则$A<\frac{π}{6}$”的逆否命题为真命题.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①根据含有量词的命题的否定进行判断.
②根据充分条件的定义进行判断.
③根据复合命题的真假关系进行判断.
④根据逆否命题的真假关系进行判断.
解答 解:①命题“?x∈(1,+∞),2x>2”的否定是“?x∈(1,+∞),2x≤2”,故①错误,
②由|a|=2,得a=2或a=-2,即“a=2”是“|a|=2”的充分不必要条件;故②错误,
③若命题p为真,命题¬q为真,则q为假命题.,则命题p∧q为假命题;故③错误,
④命题“在△ABC中,若$sinA<\frac{1}{2}$,则0<$A<\frac{π}{6}$或$\frac{5π}{6}$<A<π,则原命题为假命题,则命题的逆否命题为假命题.故④错误,
故正确的为0个,
故选:A
点评 本题主要考查命题的真假判断,涉及含有量词的命题的否定,充分条件和必要条件的判断,复合命题真假平行,以及四种命题的真假判断,涉及的知识点较多,难度不大.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
20.已知函数f(x)=x3-3x2+1,g(x)=$\left\{\begin{array}{l}{x+\frac{1}{4x},x>0}\\{-x^2-6x-8,x≤0}\end{array}\right.$,则方程g[f(x)]-1=0的根的个数为( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
4.向量$\overrightarrow{e_1},\;\overrightarrow{e_2},\;\overrightarrow a,\;\overrightarrow b$在正方形网格中的位置如图所示,则$\overrightarrow a-\overrightarrow b$=( )
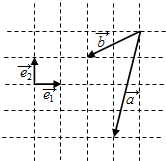

| A. | $-4\overrightarrow{e_1}-2\overrightarrow{e_2}$ | B. | $-2\overrightarrow{e_1}-4\overrightarrow{e_2}$ | C. | $\overrightarrow{e_1}-3\overrightarrow{e_2}$ | D. | $3\overrightarrow{e_1}-\overrightarrow{e_2}$ |
1.已知$sin(π+α)=-\frac{1}{2}$,那么$cos(\frac{3}{2}π+α)$=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
18.设函数$f(x)={e^{{x^2}-3x}}$(e为自然底数),则使f(x)<1成立的一个充分不必要条件是( )
| A. | 0<x<1 | B. | 0<x<4 | C. | 0<x<3 | D. | 3<x<4 |
19.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
(1)画出茎叶图;
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?
| 甲 | 27 | 37 | 29 | 36 | 33 | 30 |
| 乙 | 32 | 28 | 37 | 33 | 27 | 35 |
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?