若数列{an}成等比数列.其公比为2.则$\frac{2{a} {2}+{a} {3}}{2{a} {4}+{a} {5}}$=$\frac{1}{4}$．题目和参考答案——青夏教育精英家教网—

题目内容

19．若数列{a_n}成等比数列，其公比为2，则$\frac{2{a}_{2}+{a}_{3}}{2{a}_{4}+{a}_{5}}$=$\frac{1}{4}$．

分析利用等比数列的通项公式即可得出．

解答解：∵数列{a_n}成等比数列，其公比为2，
则$\frac{2{a}_{2}+{a}_{3}}{2{a}_{4}+{a}_{5}}$=$\frac{{a}_{1}（2q+{q}^{2}）}{{a}_{1}（2{q}^{3}+{q}^{4}）}$=$\frac{1}{{q}^{2}}$=$\frac{1}{4}$，
故答案为：$\frac{1}{4}$．

点评本题考查了等比数列的通项公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

5．把区间[1，3]n等分，所得每个小区间的长度△x等于（　　）

7．

如图的几何体中，AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．
（1）求证：AF∥平面BCE；
（2）求证：平面BCE⊥平面CDE．

14．已知等差数列{a_n}的前n项和S_n，且满足${S_{n+1}}={n^2}-n$，则a₁=（　　）

4．

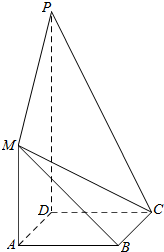如图，正方形ABCD与梯形AMPD所在的平面互相垂直，AD⊥PD，MA∥PD，MA=AD=$\frac{1}{2}$PD=1．
（Ⅰ）求证：MB∥平面PDC；
（Ⅱ）求二面角M-PC-D的余弦值；
（Ⅲ）E为线段PC上一点，若直线DE与直线PM所成的角为60°，求PE的长．

11．已知函数f（x），对于任意的x，y∈R，都有f（x+y）=f（x）+f（y），当x＞0时，f（x）＜0，且$f（1）=-\frac{1}{2}$．
（Ⅰ）求f（0），f（3）的值；
（Ⅱ）当-8≤x≤10时，求函数f（x）的最大值和最小值；
（Ⅲ）设函数g（x）=f（x²-m）-2f（|x|），判断函数g（x）最多有几个零点，并求出此时实数m的取值范围．

8．已知函数f（x）=sin$\frac{πx}{2}$（x∈R）．任取t∈R，若函数f（x）在区间[t，t+1]上的最大值为M（t），最小值为m（t），记g（t）=M（t）-m（t）．
（Ⅰ）求函数f（x）的最小正周期及对称轴方程
（Ⅱ）当t∈[-2，0]时，求函数g（t）的解析式
（Ⅲ）设函数h（x）=2^|x-k|，H（x）=x|x-k|+2k-8，其中实数k为参数，且满足关于t的不等式$\sqrt{2}$k-5g（t）≤0有解．若对任意x₁∈[4，+∞），存在x₂∈（-∞，4]，使得h（x₂）=H（x₁）成立，求实数k的取值范围
参考公式：sinα-cosα=$\sqrt{2}$sin（α-$\frac{π}{4}$）

9．下列命题中正确的个数是（　　）
①命题“?x∈（1，+∞），2^x＞2”的否定是“?x∉（1，+∞），2^x＞2”；
②“a=2”是“|a|=2”的必要不充分条件；
③若命题p为真，命题￢q为真，则命题p∧q为真；
④命题“在△ABC中，若$sinA＜\frac{1}{2}$，则$A＜\frac{π}{6}$”的逆否命题为真命题．

试题分类