题目内容
18.设函数$f(x)={e^{{x^2}-3x}}$(e为自然底数),则使f(x)<1成立的一个充分不必要条件是( )| A. | 0<x<1 | B. | 0<x<4 | C. | 0<x<3 | D. | 3<x<4 |
分析 由f(x)<1,可得x2-3x<0,解得x范围,即可判断出结论.
解答 解:由f(x)<1,可得x2-3x<0,解得0<x<3,
可得:0<x<1是使f(x)<1成立的一个充分不必要条件.
故选:A.
点评 本题考查了简易逻辑的判定方法、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
6.已知实数a,b,则“$\frac{1}{a}$>$\frac{1}{b}$”是“a<b”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
13.已知抛物线的标准方程为x2=4y,则下列说法正确的是( )
| A. | 开口向左,准线方程为x=1 | B. | 开口向右,准线方程为x=-1 | ||
| C. | 开口向上,准线方程为y=-1 | D. | 开口向下,准线方程为y=1 |
10.已知函数y=f(x)的图象是由函数$y=sin({2x+\frac{π}{6}})$的图象向左平移$\frac{π}{6}$个单位得到的,则$f({\frac{π}{3}})$=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
8.椭圆$\frac{{x}^{2}}{4}$+y2=1的两个焦点为F1,F2,过F2作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF1|等于( )
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | 4 |
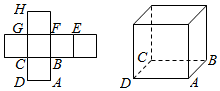 一个正方体的平面展开图及正方体的直观图的示意图如图所示:
一个正方体的平面展开图及正方体的直观图的示意图如图所示: