题目内容
8.已知函数f(x)=$\frac{1}{2}$x2-alnx(a>0)(1)若f(x)在x=2处的切线与直线 3x-2y+1=0平行,求f(x)的单调区间
(2)求f(x)在区间[1,2]上的最小值.
分析 (1)根据导数的几何意义即可求出a的值,再求出函数的定义域,求出导函数,令导函数大于0,求出x的范围,写出区间形式即得到函数f(x)的单调增区间.
(2)求出导函数,令导函数为0求出根,通过讨论根与区间[1,2]的关系,判断出函数的单调性,求出函数的最小值.
解答 解:(1)f(x)的定义域为(0,+∞),f′(x)=x-$\frac{a}{x}$=$\frac{{x}^{2}-a}{x}$,a>0,x>0
由f(x)在x=2处的切线与直线3x-2y+1=0平行,则f′(2)=$\frac{4-a}{2}$=$\frac{3}{2}$,a=1,
此时f(x)=x2-lnx,f′(x)=$\frac{{x}^{2}-1}{x}$
令f′(x)=0得x=1
f(x)与f′(x)的情况如下:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | $\frac{1}{2}$ | ↗ |
(2)由a>0及定义域为(0,+∞),令f′(x)=0得x=$\sqrt{a}$
①若$\sqrt{a}$≤1即0<a≤1在[1,2]上,f′(x)>0,
f(x)在[1,2]上单调递增,f(x)min=f(1)=$\frac{1}{2}$;
②若1<$\sqrt{a}$<2,即1<a<4在[1,$\sqrt{a}$)上,f′(x)<0,f(x)单调递减;在($\sqrt{a}$,2]上,f′(x)>0,
f(x)单调递增,因此在[1,2]上,f(x)min=f($\sqrt{a}$)=$\frac{1}{2}$a(1-lna);
③若$\sqrt{a}$≥2,即a≥4在[1,2]上,f′(x)<0,
f(x)在[1,2]上单调递减,f(x)min=f(2)=2-aln2
综上,当0<a≤1时,f(x)min=$\frac{1}{2}$;
当1<a<4时,f(x)min=$\frac{1}{2}$a(1-lna);
当a≥4时,f(x)min=2-aln2.
点评 本题考查函数的单调区间的求法、利用导数求闭区间上函数的最值,解题时要认真审题,仔细解答,注意合理地进行分类讨论思想和等价转化思想进行解题.

练习册系列答案
相关题目
5.下列四个函数中,在区间(0,+∞)上是减函数的是( )
| A. | y=log3x | B. | y=3x | C. | y=x${\;}^{\frac{1}{2}}$ | D. | y=x-1 |
20.等腰直角三角形AOB内接于抛物线y2=2px(p>0),O为抛物线的顶点,OA⊥OB,△AOB的面积是16,抛物线的焦点为F,若M是抛物线上的动点,则$\frac{|OM|}{|MF|}$的最大值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
17.执行如图所示的程序框图后,输出s的值为( )


| A. | 8 | B. | 9 | C. | 30 | D. | 36 |
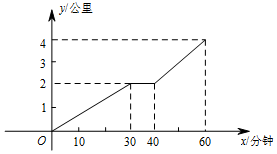 从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:
从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题: