题目内容
关于x的方程x2-mx+16=0在x∈[1，10]上有实根，则实数m的取值范围是（ ）
| A、[8，17] | ||
| B、（1，8] | ||
| C、（-∞，-8]∪[8，+∞） | ||
D、[8，
|
考点：函数的零点与方程根的关系
专题：计算题,函数的性质及应用
分析：由题意，△=m2-64≥0，故m≥8或m≤-8；再讨论即可．
解答：
解：由题意，△=m2-64≥0，
故m≥8或m≤-8；
①若m≤-8，则y=x2-mx+16在[1，10]上单调递增，
又∵1-m+16＞0，
故方程x2-mx+16=0在[1，10]上没有实根；
②若8≤m≤20，
则1-m+16≥0或100-10m+16≥0，
解得，8≤m≤17，
③若m＞20，则y=x2-mx+16在[1，10]上单调递减，
又∵1-m+16＜0，
故方程x2-mx+16=0在[1，10]上没有实根；
故选A．
故m≥8或m≤-8；
①若m≤-8，则y=x2-mx+16在[1，10]上单调递增，
又∵1-m+16＞0，
故方程x2-mx+16=0在[1，10]上没有实根；
②若8≤m≤20，
则1-m+16≥0或100-10m+16≥0，
解得，8≤m≤17，
③若m＞20，则y=x2-mx+16在[1，10]上单调递减，
又∵1-m+16＜0，
故方程x2-mx+16=0在[1，10]上没有实根；
故选A．
点评：本题考查了二次方程与二次函数之间的关系应用，属于中档题．
练习册系列答案
相关题目
若过定点M（-1，0）且斜率为k的直线与圆x2+4x+y2-5=0在第一象限内的部分有交点，则k的取值范围是（ ）
A、0＜k＜
| ||
B、-
| ||
C、0＜k＜
| ||
| D、0＜k＜5 |
已知a＞0＞b且c∈R，则下列不等式中一定成立的是（ ）
| A、a2＞b2 | ||||
| B、ac＞bc | ||||
| C、ac2＞bc2 | ||||
D、
|
若a∈{-2，0，1，
}，则方程x2+y2+ax+2ay+2a2+a-1=0表示的圆的个数为（ ）
| 3 |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
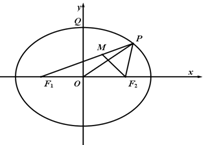如图所示，已知椭圆