Question

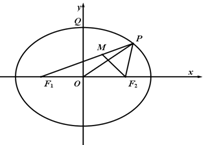如图所示，已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右焦点分别为F₁（-1，0），F₂（1，0），P为椭圆上一点，Q为上顶点，

F1M

=2

MP

，

PO

•

F2M

=0．
（1）当椭圆离心率e=

1

2

时，若直线过点（0，-

3

7

）且与椭圆交于A，B（不同于Q）两点，求∠AQB；
（2）求椭圆离心率e的取值范围．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：（1）利用已知条件求出a=2，求出椭圆的方程设AB所在的直线方程为y=kx-

3

7

，代入椭圆方程，设A（x₁，y₁），B（x₂，y₂），利用韦达定理，以及向量是数量积为0，即可求出∠AQB=

π

2

．
（2）通过

PO

•

F2M

=0，在△F₁PF₂中，由余弦定理，结合a-c≤|

PF2

|≤a+c，推出a≤2c，然后求出离心率的范围．

解答： 解：（1）c=1，e=

c

a

=

1

2

，得a=2，∴b²=a²-c²=3，
所以椭圆的方程为

x2

4

+

y2

3

=1．依题意可设AB所在的直线方程为y=kx-

3

7

，代入椭圆方程，得(3+4k2)x2-

8 3

7

kx-

576

49

=0．
设A（x₁，y₁），B（x₂，y₂），则x1+x2=

8 3 k

7(3+4k2)

，x1x2=

-576

49(3+4k2)

．
因为Q(0，

3

)，
∴

QA

•

QB

=(x1，y1-

3

)•(x2，y2-

3

)=(x1，kx1-

8 3

7

)•(x2，kx2-

8 3

7

)
=(1+k2)x1x2-

8 3

7

k(x1+x2)+

192

49

=(1+k2)

-576

49(3+4k2)

-

8 3

7

k

8 3 k

7(3+4k2)

+

192

49

=

-576-576k2-192k2+576+768k2

49(3+4k2)

=0，
所以∠AQB=

π

2

．
（2）因为

PO

=

1

2

(

PF1

+

PF2

)，

F2M

=

PM

-

PF2

=

1

3

PF1

-

PF2

，
因为

PO

•

F2M

=0，所以

1

2

(

PF1

+

PF2

)•(

1

3

PF1

-

PF2

)=0，化简得

PF1

2-2

PF1

•

PF2

-3

PF2

2=0，即|

PF1

|2-2|

PF1

||

PF2

|cos∠F1PF2-3|

PF2

|2=0，
在△F₁PF₂中，由余弦定理，有|

PF1

|2+|

PF2

|2-2|

PF1

||

PF2

|cos∠F1PF2=4c2，
所以4|

PF2

|2=4c2，|

PF2

|=c，又因为a-c≤|

PF2

|≤a+c，∴a≤2c，
即e=

c

a

≥

1

2

，∵0＜e＜1∴e∈[

1

2

，1)．

点评：本题考查椭圆的综合应用，椭圆的基本性质的应用，考查分析问题解决问题的能力．