题目内容
10.已知函数f(x+$\frac{1}{2}$)为奇函数,设g(x)=f(x)+1,则g($\frac{1}{2016}$)+g($\frac{2}{2016}$)+…+g($\frac{2015}{2016}$)=2015.分析 由已知可得f(x)+f(1-x)=0,进而g(x)+g(1-x)=2,进而得到答案.
解答 解:∵函数f(x+$\frac{1}{2}$)为奇函数,
故f(x)+f(1-x)=0,
∵g(x)=f(x)+1,
∴g(x)+g(1-x)=2,
故2[g($\frac{1}{2016}$)+g($\frac{2}{2016}$)+…+g($\frac{2015}{2016}$)]=2×2015,
即g($\frac{1}{2016}$)+g($\frac{2}{2016}$)+…+g($\frac{2015}{2016}$)=2015,
故答案为:2015.
点评 本题考查的知识点是抽象函数及其应用,函数的奇偶性,函数求值,难度中档.

练习册系列答案
相关题目
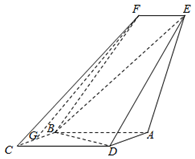 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.