题目内容
15.A是集合{1,2,3,…,14}的子集,从A中任取3个元素,由小到大排列之后都不能构成等差数列,则A中元素个数的最大值是8.分析 根据A是集合{1,2,3,…,14}的子集,从A中任取3个元素,由小到大排列之后都不能构成等差数列,列举出满足条件的集合A中元素,可得答案.
解答 解:若1∈A,2∈A,
根据从A中任取3个元素,由小到大排列之后都不能构成等差数列可得:
3∉A,
令4∈A,5∈A,
则6∉A,7∉A,
令8∈A,
则9∉A,
令10∈A,11∈A,
则12∉A,
令13∈A,
则14∉A,
此时A中元素个数取最大值,
故答案为:8
点评 本题考查等差数列的定义,推理与证明,难度中档.

练习册系列答案
相关题目
11.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=3x+1-3,则f(-1)的值为( )
| A. | -6 | B. | -3 | C. | -2 | D. | 6 |
20.(x-a)10的展开式中,x7的系数为15,则实数a=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{8}$ | D. | $\frac{1}{8}$ |
7.某人提出一个问题,甲先答,答对的概率为0.4,如果甲答错,由乙答,答对的概率为0.5,则问题由乙答对的概率为 ( )
| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.8 |
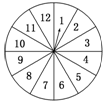 某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如下图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.
某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如下图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.