题目内容
5．在四边形ABCD中，∠A=135°，∠B=∠D=90°，BC=2$\sqrt{3}$，AD=2，则四边形ABCD的面积是4．分析 作辅作线，构造直角三角形，根据题中所给的条件，在直角三角形中解题，根据角的正弦值与三角形边的关系，可求出各边的长，然后四边形ABCD的面积．
解答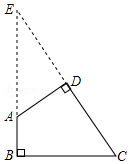 
解：如图，分别延长CD，BA交于点E．
∵∠DAB=135°，
∴∠EAD=∠C=∠E=45°，
∴BE=BC=2，AD=ED=2，
∴四边形ABCD的面积=S△EBC-S△ADE=$\frac{1}{2}$BC•BE-$\frac{1}{2}$AD•DE，
=$\frac{1}{2}$×2 $\sqrt{3}$×2$\sqrt{3}$-$\frac{1}{2}$×2×2，
=6-2，
=4．
故答案为：4
点评 本题通过“割补法”求图形的面积，是解决不规则图形面积问题的基本方法．
练习册系列答案
相关题目
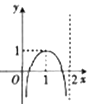
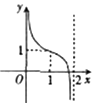
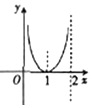
19．函数$f（x）=Asin（ωx+φ），（ω＞0，-\frac{π}{2}＜φ＜\frac{π}{2}）$的部分图象如图所示，则A，ω，φ的值分别是（ ）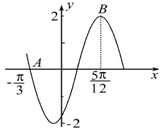
| A． | 1，$2，-\frac{π}{6}$ | B． | 2，$2，-\frac{π}{3}$ | C． | 1，$4，-\frac{π}{6}$ | D． | 2，$4，\frac{π}{3}$ |
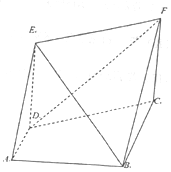如图所示，直角梯形ABCD中，AD∥BC，AD⊥AB，AB=BC=2AD=2，四边形EDCF为矩形，CF=$\sqrt{3}$，平面EDCF⊥平面ABCD．