题目内容
19.已知过原点O的圆x2+y2-2ax=0又过点(4,2),(1)求圆的方程,(2)A为圆上动点,求弦OA中点M的轨迹方程.分析 (1)(4,2)代入圆x2+y2-2ax=0,可得a=2.5,即可求圆的方程;
(2)设出M点坐标为(x,y),求出A点坐标是,利用A点坐标满足圆的方程,代入求解可得弦OA中点M的轨迹方程
解答 解:(1)(4,2)代入圆x2+y2-2ax=0,可得a=2.5,
∴圆的方程为x2+y2-5x=0;
(2)设M点坐标为(x,y),那么A点坐标是(2x,2y),
A点坐标满足圆x2+y2-5x=0的方程,
所以(2x)2+(2y)2-10x=0
所以M点轨迹方程为x2+y2-2.5x=0.
点评 本题是中档题,考查曲线轨迹方程的求法,注意中点坐标的灵活运用,本题是应用代入法求解的,注意掌握.

练习册系列答案
相关题目
14.已知两个不同的平面α,β和两条不重合的直线m,n,则下列四个命题中不正确的是( )
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m⊥α,m⊥β,则α∥β | ||
| C. | 若m⊥α,m∥n,n?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |
11.用数学归纳法证明1+a+a2+…+an+1=$\frac{{1-{a^{n+2}}}}{1-a}({a≠0,1,n∈{N^*}})$,在验证n=1成立时,计算左边所得的项是( )
| A. | 1 | B. | 1+a | C. | a2 | D. | 1+a+a2 |
1.已知数列{an}为等比数列,其中a5,a9为方程x2+2016x+9=0的二根,则a7的值( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 9 |
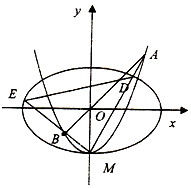 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的短轴长,C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于点D、E.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的短轴长,C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于点D、E.