题目内容
20.已知直线l:4x-3y+6=0,抛物线x=$\frac{1}{4}{y^2}$上一动点P到y轴和直线l的距离之和的最小值是1.分析 作图,化点P到直线l:2x-y+3=0和y轴的距离之和为PF+PA-1,从而求最小值.
解答 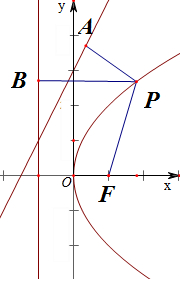 解:由题意抛物线x=$\frac{1}{4}{y^2}$,可知y2=4x,准线方程x=-1,
解:由题意抛物线x=$\frac{1}{4}{y^2}$,可知y2=4x,准线方程x=-1,
作图如右图,点P到直线l:4x-3y+6=0为PA;
点P到y轴的距离为PB-1;
而由抛物线的定义知,
PB=PF;
故点P到直线l:4x-3y+6=0和y轴的距离之和为PF+PA-1;
而点F(1,0)到直线l:4x-3y+6=0的距离为:
$\frac{|4+6|}{\sqrt{{4}^{2}+{3}^{2}}}$=2;
故点P到直线l:4x-3y+6=0和y轴的距离之和的最小值为2-1=1;
故答案为:1.
点评 本题考查了学生的作图能力及圆锥曲线的定义应用,属于中档题.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
11.下列事件:
(1)口袋里有伍角、壹角、壹元的硬币若干枚,随机地摸出一枚是壹角;
(2)在标准大气压下,水在90℃沸腾;
(3)射击运动员射击一次命中10环;
(4)同时掷两颗骰子,出现的点数之和不超过12,
其中是随机事件的有( )
(1)口袋里有伍角、壹角、壹元的硬币若干枚,随机地摸出一枚是壹角;
(2)在标准大气压下,水在90℃沸腾;
(3)射击运动员射击一次命中10环;
(4)同时掷两颗骰子,出现的点数之和不超过12,
其中是随机事件的有( )
| A. | (1) | B. | (1)(2) | C. | (1)(3) | D. | (2)(4) |
12.已知函数f(x)=x3-px2-qx的图象与x轴切于(1,0)点,则f(x)在[-1,1]的最大值、最小值分别为( )
| A. | 0,-4 | B. | $\frac{4}{27}$,-4 | C. | $\frac{4}{27}$,0 | D. | 2,0 |
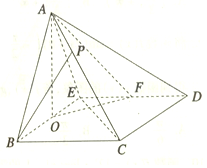 在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.
在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.