题目内容
不经过原点O的直线l与圆x2+y2=1交于不同的两点P、Q,若直线PQ的斜率是直线OP和直线OQ斜率的等比中项,则S△POQ的取值范围为 .
考点:直线与圆的位置关系
专题:综合题,直线与圆
分析:设直线l的方程为y=kx+m代入圆的方程消去y得,(1+k2)x2+2kmx+m2-1=0,由此利用根的判别式、韦达定理、等比数列结合已知条件能求出k.直线OQ的斜率存在且不为0,及△>0,得0<m2<2,且m≠1,求出点O到直线l的距离,由此能求出S△OPQ的取值范围.
解答:
解:由题意可知,直线l的斜率存在且不为0,故可设直线l的方程为y=kx+m(m≠0)
P(x1,y1),Q(x2,y2)
由y=kx+m,代入圆的方程消去y得,(1+k2)x2+2kmx+m2-1=0
则△=(2km)2-4(1+k2)×(m2-1)=4(k2-m2+1)>0
且x1+x2=-
,x1x2=
故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2
因为直线OP,PQ,OQ的斜率依次成等比数列,
所以
•
=k2,
所以1-k2=0
所以直线l的斜率k为±1
直线OQ的斜率存在且不为0,及△>0
所以0<m2<2,且m≠1,
设d为点O到直线l的距离,
则S△OPQ=
d|PQ|=
|m|
=
≤
∴S△OPQ的取值范围为(0,
].
故答案为:(0,
].
P(x1,y1),Q(x2,y2)
由y=kx+m,代入圆的方程消去y得,(1+k2)x2+2kmx+m2-1=0
则△=(2km)2-4(1+k2)×(m2-1)=4(k2-m2+1)>0
且x1+x2=-
| 2km |
| 1+k2 |
| m2-1 |
| 1+k2 |
故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2
因为直线OP,PQ,OQ的斜率依次成等比数列,
所以
| y1 |
| x1 |
| y2 |
| x2 |
所以1-k2=0
所以直线l的斜率k为±1
直线OQ的斜率存在且不为0,及△>0
所以0<m2<2,且m≠1,
设d为点O到直线l的距离,
则S△OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
| 1 |
| 2 |
| m2(2-m2) |
| 1 |
| 2 |
∴S△OPQ的取值范围为(0,
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |
点评:本题考查直线的斜率的求法,考查三角形面积的取值范围的求法,解题时要认真审题,注意弦长公式的合理运用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
计算:
=( )
| 2i |
| i-1 |
| A、i+1 | B、i-1 |
| C、-i+1 | D、-i-1 |
函数f(x)=2sin(2x+
)的增区间为( )
| π |
| 6 |
A、[kπ-
| ||||
B、[kπ+
| ||||
C、[kπ-
| ||||
D、[kπ-
|
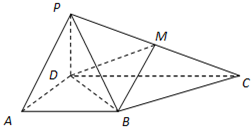 如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB,PD⊥底面ABCD,M为PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB,PD⊥底面ABCD,M为PC的中点.