题目内容
12．已知复数z=（2+i）（a+2i3）在复平面内对应的点在第四象限，则实数a的取值范围是（ ）| A． | （-∞，-1） | B． | （4，+∞） | C． | （-1，4） | D． | （-4，-1） |
分析 利用复数的运算法则、不等式的解法、几何意义即可得出．
解答 解：复数z=（2+i）（a+2i3）=（2+i）（a-2i）=2a+2+（a-4）i，
在复平面内对应的点（2a+2，a-4）在第四象限，则2a+2＞0，a-4＜0，
解得-1＜a＜4．
实数a的取值范围是（-1，4）．
故选：C．
点评 本题考查了复数的运算法则、几何意义、不等式的解法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
2．函数$f（x）=\frac{1}{2}cos（ωx+φ）$（ω＞0，$|φ|＜\frac{π}{2}$）的部分图象如图所示，则φ的值为（ ）
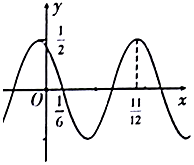
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $-\frac{π}{6}$ | D． | $-\frac{π}{3}$ |
3．已知向量$\overrightarrow{a}$=（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$），$\overrightarrow{b}$=（$\sqrt{3}$，-1），则$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{2π}{3}$ |
7．已知复数$z=\frac{{a+2{i^3}}}{2-i}$在复平面内对应的点在第四象限，则实数a的取值范围是（ ）
| A． | （-∞，-1） | B． | （4，+∞） | C． | （-1，4） | D． | （-4，-1） |
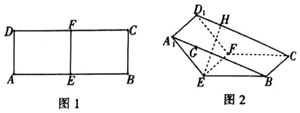如图1，在矩形ABCD中，AB=8，AD=3，点E，F分别为AB、CD的中点，将四边形AEFD沿EF折到A1EFD1的位置，使∠A1EB=120°，如图2所示，点G、H分别在A1B、D1C上，A1G=D1H=$\sqrt{3}$，过点G、H的平面α与几何体A1EB-D1FC的面相交，交线围成一个正方形．
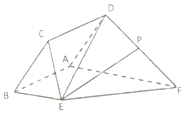如图，已知菱形ABCD与直角梯形ABEF所在的平面互相垂直，其中BE∥AF，∠EBA=90°，AB=BE=$\frac{1}{2}$AF=2，∠CBA=$\frac{π}{3}$，P为DF的中点．
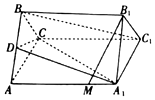如图，在正三棱柱ABC-A1B1C1中，点D是AB的上一点，且AD=tAB．