题目内容
1.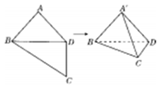 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )| A. | A'C⊥BD | B. | 四面体 A'-BCD的体积为 $\frac{1}{3}$ | ||
| C. | CA'与平面 A'BD所成的角为 30° | D. | ∠BA'C=90° |
分析 折叠前AB⊥AD,折叠后CD⊥平面A'BD,取BD的中点O,推导出A'O⊥平面BCD,OC不垂直于BD.由此能求出结果.
解答 解:折叠前AB=AD=1,BD=$\sqrt{2}$,即AB⊥AD,
折叠后平面A'BD⊥平面BCD,且CD⊥BD,
故CD⊥平面A'BD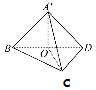 ,取BD的中点O,∵A'B=A'D,
,取BD的中点O,∵A'B=A'D,
∴A'O⊥BD.又平面A'BD⊥平面BCD,平面A'BD∩平面BCD=BD,
∴A'O⊥平面BCD.
∵CD⊥BD,
∴OC不垂直于BD.假设A'C⊥BD,
∵OC为A'C在平面BCD内的射影,
∴OC⊥BD,矛盾,∴A'C不垂直于BD,故A错误;
∵CD⊥BD,平面A'BD⊥平面BCD,
∴CD⊥平面A'BD,A'C在平面A'BD内的射影为A'D.
∵A'B=A'D=1,BD=$\sqrt{2}$,
∴A'B⊥A'D,A'B⊥A'C,B正确,
∠CA'D为直线CA'与平面A'BD所成的角,
∠CA'D=45°,故C错误;
VA'-BCD=VC-A'BD=$\frac{1}{3}$S△A'BD•CD=$\frac{1}{6}$,故B错误.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
12.高三某班要安排6名同学值日(周日休息),每天安排一人,每人值日一天,要求甲必须安排在周一到周四的某一天,乙必须安排在周五或周六的某一天,则不同的值日生表有多少种?( )
| A. | 144 | B. | 192 | C. | 360 | D. | 720 |
9.若全集U={1,2,3,4,5},集合M={1,2},N={2,3,4},则(∁UM)∩N等于( )
| A. | {1} | B. | {2} | C. | {3,4} | D. | {5} |
10.已知a=${∫}_{0}^{\frac{π}{2}}$(-cosx)dx,则(ax+$\frac{1}{ax}$)9展开式中,x3项的系数为( )
| A. | $\frac{63}{8}$ | B. | $\frac{63}{16}$ | C. | -84 | D. | -$\frac{63}{8}$ |