题目内容
6.已知函数f(x)=(x-1)ex.(1)求f(x)的单调区间;
(2)求f(x)在区间[0,1]上的最大值与最小值.
分析 (1)求出函数的导数,由导数大于0,可得增区间;由导数小于0,可得减区间;
(2)由(1)可得f(x)在[0,1]递增,即可得到所求的最值.
解答 解:(1)f(x)=(x-1)ex的导数为f′(x)=xex,
令f′(x)=0,得x=0.
f(x)与f′(x)的情况如下:
| x | (-∞,0) | 0 | (0,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 减 | -1 | 增 |
(2)由(1)函数f(x)的递增区间为(0,+∞),
所以函数f(x)在[0,1]上单调递增,
所以当x=0时,f(x)有最小值f(0)=-1;
当x=1时,f(x)有最大值f(1)=0.
点评 本题考查导数的运用:求单调区间和最值,考查函数的单调性的运用:求最值,考查运算能力,属于基础题.

练习册系列答案
相关题目
16.已知命题P:?x∈R,ex-x-1>0,则¬P是( )
| A. | ?x∈R,ex-x-1<0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≤0 | ||
| C. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1<0 | D. | ?x∈R,ex-x-1≤0 |
14.在△ABC中,若a2=b2+c2-$\sqrt{3}$bc,则角A的度数为( )
| A. | 30° | B. | 150° | C. | 60° | D. | 120° |
1.已知△ABC中,sinA=$\frac{12}{13}$且A是锐角,则cosA=( )
| A. | $\frac{12}{13}$ | B. | $\frac{5}{13}$ | C. | -$\frac{5}{13}$ | D. | -$\frac{12}{13}$ |
18.设点A为双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1的右顶点,则点A到该双曲线的一条渐近线的距离是( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
16.一个几何体的三视图如图所示,则这个几何体的体积等于( )
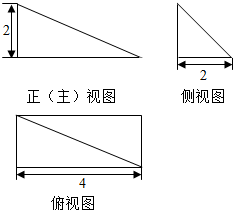

| A. | 12 | B. | 4 | C. | $\frac{16}{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
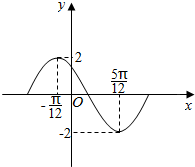 函数y=Asin(ωx+ϕ),(A>0,ω>0,0<ϕ<π)在一个周期内的图象如图所示.
函数y=Asin(ωx+ϕ),(A>0,ω>0,0<ϕ<π)在一个周期内的图象如图所示.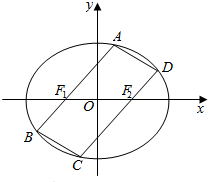 已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为$\frac{1}{2}$,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.
已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为$\frac{1}{2}$,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.