题目内容
已知
=-2,则
=( )
| lim |
| x→4 |
| f(x)-f(4) |
| x-4 |
| lim |
| t→0 |
| f(4-t)-f(4) |
| 2t |
| A、4 | B、-4 | C、1 | D、-1 |
考点:极限及其运算
专题:计算题
分析:令x-4=t,求出当t趋于0是f(4)的极限值,把要求的式子变形后得答案.
解答:
解:令x-4=t,则x=4+t,
由
=-2,
得
=-2,
∴
=
=-
=-
×(-2)=1.
故选:C.
由
| lim |
| x→4 |
| f(x)-f(4) |
| x-4 |
得
| lim |
| t→0 |
| f(4+t)-f(4) |
| t |
∴
| lim |
| t→0 |
| f(4-t)-f(4) |
| 2t |
| lim |
| t→0 |
| f(4+t)-f(4) |
| -2t |
| 1 |
| 2 |
| lim |
| t→0 |
| f(4+t)-f(4) |
| t |
| 1 |
| 2 |
故选:C.
点评:本题考查了极限及其运算,考查了换元思想方法,解答的关键是化为求变量趋于0时的极限值,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
不等式2x-y+5>0表示的区域在直线2x-y+5=0的( )
| A、右上方 | B、右下方 |
| C、左上方 | D、左下方 |
若△ABC的三个内角满足SinA:sinB:SinC=6:12:15,则△ABC( )
| A、一定是锐角三角形 |
| B、一定是直角三角形 |
| C、一定是钝角三角形 |
| D、可能是锐角三角形也可能是钝角三角形 |
下列函数中,既是奇函数又在区间(0,+∞)上单调递增的是( )
A、y=x+
| ||
| B、y=ex-e-x | ||
| C、y=x3-x | ||
| D、y=xlnx |
 已知
已知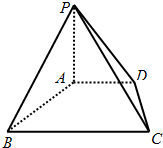 已知四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AB=BC=2AD,若平面PCD与平面PAB所成二面角的余弦值为
已知四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AB=BC=2AD,若平面PCD与平面PAB所成二面角的余弦值为