题目内容
19.已知实数x、y满足$\left\{\begin{array}{l}{x≥1}\\{y≤2}\\{x-y≤0}\end{array}\right.$,则目标函数z=x+|2x-y-1|的最大值为3.分析 作出不等式组对应的平面区域,和直线2x-y-1=0,分2x-y-1≤0和2x-y-1>0,利用数形结合进行求解即可.
解答 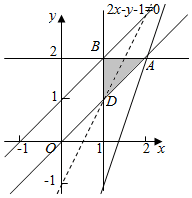 解:作出不等式组对应的平面区域以及直线2x-y-1=0的图象,
解:作出不等式组对应的平面区域以及直线2x-y-1=0的图象,
当阴影部分在直线2x-y-1=0的左上方时
即此时2x-y-1≤0,
则z=x+|2x-y-1|=x-(2x-y-1)=-x+y+1,
即y=x+z-1,
平移直线y=x+z-1,当直线y=x+z-1经过点B(1,2)上,直线y=x+z-1的截距最大,
此时z最大,为z=-1+2+1=2,
当阴影部分在直线2x-y-1=0的右下方时,即2x-y-1>0时,
z=x+|2x-y-1|=x+(2x-y-1)=3x-y-1,
即y=3x-z-1,
平移直线y=3x-z-1,当直线y=3x-z-1经过点A(2,2)上,直线y=x+z-1的截距最小,
此时z最大,为z=6-2-1=3,
综上z的最大值为3,
故答案为:3.
点评 本题主要考查线性规划的应用,根据条件确定2x-y-1≤0和2x-y-1>0,去掉绝对值,利用数形结合是解决本题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
7.$\frac{sin87°-cos63°cos60°}{cos27°}$等于( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |