题目内容
4.已知函数f(x)=3sinx+mcosx(m<0),当x=α时,f(x)取得最大值5,则tanα的值为-$\frac{3}{4}$.分析 化简函数f(x)=3sinx+mcosx为一个角的一个三角函数的形式,由已知可得$\sqrt{9+{m}^{2}}$sin(α+θ)=5,解得m,α=2kπ+$\frac{π}{2}$-θ,k∈Z,利用诱导公式即可解得tanα的值.
解答 解:∵函数f(x)=3sinx+mcosx=$\sqrt{9+{m}^{2}}$sin(x+θ),其中tanθ=$\frac{m}{3}$,
∵当x=α时,f(x)取得最大值5,可得:$\sqrt{9+{m}^{2}}$sin(α+θ)=5,
∴$\sqrt{9+{m}^{2}}$=5,m<0,解得:m=-4,
∴α+θ=2kπ+$\frac{π}{2}$,k∈Z,解得:α=2kπ+$\frac{π}{2}$-θ,k∈Z,
∴tanα=tan($\frac{π}{2}$-θ)=cotθ=$\frac{3}{m}$=-$\frac{3}{4}$.
故答案为:-$\frac{3}{4}$.
点评 本题主要考查了两角和的正弦函数公式,正弦函数的最值的应用,考查了诱导公式的应用,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
14.阅读如图所示的程序框图,运行相应的程序.则输出的S=( )
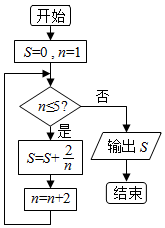

| A. | $\frac{8}{3}$ | B. | $\frac{46}{15}$ | C. | $\frac{25}{6}$ | D. | $\frac{137}{30}$ |
8.若实数a=20.1,b=log32,c=log0.34,则a,b,c的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
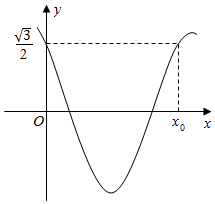 已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.