题目内容
9.已知向量$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{c}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,则$\overrightarrow{c}$=$-\frac{1}{8}\overrightarrow{a}$$+\frac{5}{8}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).分析 可设$\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}$,进行向量数乘运算便可得出$\overrightarrow{c}=(2x+2y)\overrightarrow{{e}_{1}}+(3x-y)\overrightarrow{{e}_{2}}$,这样根据平面向量基本定理便可得出关于x,y的二元一次方程组,解出x,y,从而可用$\overrightarrow{a},\overrightarrow{b}$表示出$\overrightarrow{c}$.
解答 解:设$\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}=x(2\overrightarrow{{e}_{1}}+3\overrightarrow{{e}_{2}})$$+y(2\overrightarrow{{e}_{1}}-\overrightarrow{{e}_{2}})$=$(2x+2y)\overrightarrow{{e}_{1}}+(3x-y)\overrightarrow{{e}_{2}}$;
又$\overrightarrow{c}=\overrightarrow{{e}_{1}}-\overrightarrow{{e}_{2}}$;
∴由平面向量基本定理得,$\left\{\begin{array}{l}{2x+2y=1}\\{3x-y=-1}\end{array}\right.$;
解得$\left\{\begin{array}{l}{x=-\frac{1}{8}}\\{y=\frac{5}{8}}\end{array}\right.$;
∴$\overrightarrow{c}=-\frac{1}{8}\overrightarrow{a}+\frac{5}{8}\overrightarrow{b}$.
故答案为:$-\frac{1}{8}\overrightarrow{a}+\frac{5}{8}\overrightarrow{b}$.
点评 考查向量的数乘运算,以及平面向量基本定理.

| A. | 2n | B. | 2n | C. | 2n+1-2 | D. | n2+n |
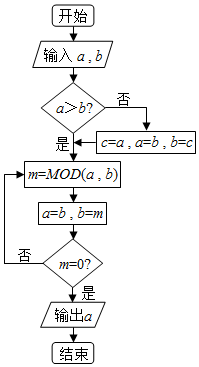
| A. | 0 | B. | 17 | C. | 21 | D. | 34 |
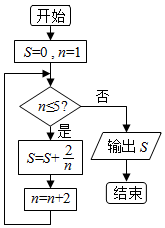
| A. | $\frac{8}{3}$ | B. | $\frac{46}{15}$ | C. | $\frac{25}{6}$ | D. | $\frac{137}{30}$ |