题目内容
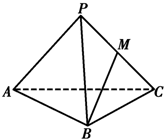
 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.(1)证明:SD⊥平面SAB
(2)求AB与平面SBC所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)取AB中点E,连结DE,证明SD⊥平面SAB,只需证明SD⊥SE,AB⊥SD;
(2)求出F到平面SBC的距离,由于ED∥BC,所以ED∥平面SBC,可得E到平面SBC的距离,从而可求AB与平面SBC所成角的正弦值.
(2)求出F到平面SBC的距离,由于ED∥BC,所以ED∥平面SBC,可得E到平面SBC的距离,从而可求AB与平面SBC所成角的正弦值.
解答:
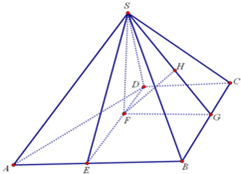 (1)证明:取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2.
(1)证明:取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2.
连结SE,则SE⊥AB,SE=
又SD=1,故ED2=SE2+SD2
所以∠DSE为直角,
所以SD⊥SE,
由AB⊥DE,AB⊥SE,DE∩SE=E,得AB⊥平面SDE,所以AB⊥SD.
因为AB∩SE=E,
所以SD⊥平面SAB…6分
(2)解:由AB⊥平面SDE知,平面ABCD⊥平面SDE.
作SF⊥DE,垂足为F,则SF⊥平面ABCD,SF=
=
作FG⊥BC,垂足为G,则FG=DC=1.
连结SG,则SG⊥BC
又FG⊥BC,SG∩FG=G,
故BC⊥平面SFG,平面SBC⊥平面SFG,
作FH⊥SG,H为垂足,则FH⊥平面SBC,FH=
=
即F到平面SBC的距离为
.
由于ED∥BC,所以ED∥平面SBC,E到平面SBC的距离d也为
.
设AB与平面SBC所成的角为α,则sinα=
=
…12分.
 (1)证明:取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2.
(1)证明:取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2.连结SE,则SE⊥AB,SE=
| 3 |
又SD=1,故ED2=SE2+SD2
所以∠DSE为直角,
所以SD⊥SE,
由AB⊥DE,AB⊥SE,DE∩SE=E,得AB⊥平面SDE,所以AB⊥SD.
因为AB∩SE=E,
所以SD⊥平面SAB…6分
(2)解:由AB⊥平面SDE知,平面ABCD⊥平面SDE.
作SF⊥DE,垂足为F,则SF⊥平面ABCD,SF=
| SD×SE |
| DE |
| ||
| 2 |
作FG⊥BC,垂足为G,则FG=DC=1.
连结SG,则SG⊥BC
又FG⊥BC,SG∩FG=G,
故BC⊥平面SFG,平面SBC⊥平面SFG,
作FH⊥SG,H为垂足,则FH⊥平面SBC,FH=
| SF×FG |
| SG |
| ||
|
即F到平面SBC的距离为
| ||
| 7 |
由于ED∥BC,所以ED∥平面SBC,E到平面SBC的距离d也为
| ||
| 7 |
设AB与平面SBC所成的角为α,则sinα=
| d |
| EB |
| ||
| 7 |
点评:本题考查线面垂直,考查线面角,考查学生分析解决问题的能力,考查学生的计算能力,正确求出E到平面SBC的距离是关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知sinα=m(|m|<1),
<α<π,那么tanα=( )
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、±
| ||||
D、±
|
已知数列{an}满足a1=1且
=
,则a2013=( )
| an+1 |
| an |
| n+1 |
| n |
| A、2010 | B、2011 |
| C、2012 | D、2013 |
函数f(x)=
+
的定义域为( )
| x2-4 |
| 1 |
| x-3 |
| A、[2,+∞)∪(-∞,-2] |
| B、[2,3)∪(3,+∞) |
| C、[2,3)∪(3,+∞)∪(-∞,-2] |
| D、(-∞,-2] |