题目内容
如图:四面体P-ABC为正四面体,M为PC的中点,则BM与AC所成的角的余弦值为 .
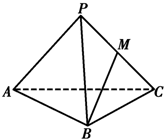

考点:异面直线及其所成的角
专题:计算题,空间角
分析:取AP的中点N,连结MN、BN,根据三角形中位线定理可得MN∥AC且MN=
AC,因此∠NMB(或其补角)就是BM与AC所成的角.然后在△BMN中由余弦定理加以计算,即可得出BM与AC所成的角的余弦值.
| 1 |
| 2 |
解答:
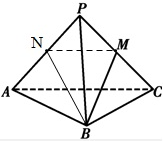 解:取AP的中点N,连结MN、BN,可得
解:取AP的中点N,连结MN、BN,可得
∵△PAC中,MN是中位线,
∴MN∥AC且MN=
AC.
因此∠NMB(或其补角)就是BM与AC所成的角.
设正四面体P-ABC的棱长为2,
则△BMN中,MN=
AC=1,BN=BM=
,
∴由余弦定理,可得cos∠NMB=
=
,
由此可得BM与AC所成的角的余弦值为
故答案为:
 解:取AP的中点N,连结MN、BN,可得
解:取AP的中点N,连结MN、BN,可得∵△PAC中,MN是中位线,
∴MN∥AC且MN=
| 1 |
| 2 |
因此∠NMB(或其补角)就是BM与AC所成的角.
设正四面体P-ABC的棱长为2,
则△BMN中,MN=
| 1 |
| 2 |
| 3 |
∴由余弦定理,可得cos∠NMB=
| 1+3-3 | ||
2×1×
|
| ||
| 6 |
由此可得BM与AC所成的角的余弦值为
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本题在正四面体中求异面直线所成角的余弦值,着重考查了正四面体的性质、异面直线所成角的定义及其求法等知识,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
设f(x)定义在实数集R上的函数,满足条件y=f(x+1)是偶函数,且当x≥1时,f(x)=(
)x-1,则f(
),f(
),f(
)的大小关系是( )
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
A、f(
| ||||||
B、f(
| ||||||
C、f(
| ||||||
D、f(
|
已知
(
-an)=b,则常数a、b的值分别为( )
| lim |
| n→∞ |
| 2n2 |
| 2+n |
| A、a=2,b=-4 | ||||
| B、a=-2,b=4 | ||||
C、a=
| ||||
D、a=-
|
已知直线l1:ax+2y+6=0与l2:x+(a-1)y+a2-1=0平行,则实数a的值是( )
| A、-1或2 | B、0或1 |
| C、-1 | D、2 |
一个几何体的三视图如图所示,其中俯视图是一个菱形,则该几何体的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.