题目内容
若曲线y=
,与直线y=kx-1有两个不同的交点,则实数k的取值范围是( )
|
A、(3-2
| ||||
B、(0,3-2
| ||||
C、(-∞,0)∪(0,3-2
| ||||
D、(-∞,3-2
|
考点:分段函数的应用
专题:函数的性质及应用
分析:作出两个函数的图象,利用数形结合即可得到结论.
解答:
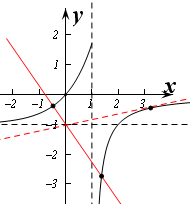 解:作出曲线y=
解:作出曲线y=
的图象如图:
直线y=kx-1过定点(0,-1),
当k=0时,两个函数只有一个交点,不满足条件,
当k<0时,两个函数有2个交点,满足条件,
当k>0时,直线y=kx-1与y=
在x>1相切时,两个函数只有一个交点,此时
=kx-1,即kx2+(1+k)x+2=0,
判别式△=(1+k)2-8k=0,解得k2-6k+1=0,
解得k=
=
=3+2
或k=
=
=3-2
(舍去),
则此时满足0<k<3+2
,
综上满足条件的k的取值范围是(-∞,0)∪(0,3-2
),
故选:C
 解:作出曲线y=
解:作出曲线y=
|
直线y=kx-1过定点(0,-1),
当k=0时,两个函数只有一个交点,不满足条件,
当k<0时,两个函数有2个交点,满足条件,
当k>0时,直线y=kx-1与y=
| 1 |
| 1-x |
| 1 |
| 1-x |
判别式△=(1+k)2-8k=0,解得k2-6k+1=0,
解得k=
6+
| ||
| 2 |
6+4
| ||
| 2 |
| 2 |
或k=
6-
| ||
| 2 |
6-4
| ||
| 2 |
| 2 |
则此时满足0<k<3+2
| 2 |
综上满足条件的k的取值范围是(-∞,0)∪(0,3-2
| 2 |
故选:C
点评:本题主要考查函数与方程的应用,利用数形结合以及分段函数的性质是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=|lgx|-(
)x的零点个数为( )
| 1 |
| 2 |
| A、3 | B、0 | C、1 | D、2 |
已知
=(-3,4)与
=(6,x)共线,则x=( )
| a |
| b |
| A、8 | ||
| B、-8 | ||
C、
| ||
D、-
|
如果25,x,y,z,1成等比数列,那么( )
| A、y=5,xz=25 |
| B、y=-5,xz=25 |
| C、y=5,xz=-25 |
| D、y=-5,xz=-25 |
圆锥的底面半径为1,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | ||||
| B、5π | ||||
| C、3π | ||||
D、
|
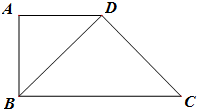 如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题:
如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题: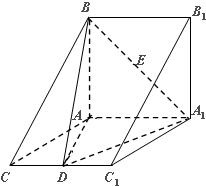 如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.
如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.
