题目内容
 如图,过抛物线y2=2px(p>0)的焦点F的两条互相垂直的直线与抛物线分别交于点A、B和C、D;抛物线上的点T(2,t)(t>0)到焦点的距离为3.
如图,过抛物线y2=2px(p>0)的焦点F的两条互相垂直的直线与抛物线分别交于点A、B和C、D;抛物线上的点T(2,t)(t>0)到焦点的距离为3.(1)求p、t的值;
(2)当四边形ACBD的面积取得最小值时,求直线AB的斜率.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)利用抛物线的定义求出p、代入点的坐标代入抛物线方程求出t的值;
(2)利用抛物线方程求出AB的距离CD的距离,表示出四边形ACBD的面积,利用基本不等式求出面积的最小值,并且求出直线AB的斜率.
(2)利用抛物线方程求出AB的距离CD的距离,表示出四边形ACBD的面积,利用基本不等式求出面积的最小值,并且求出直线AB的斜率.
解答:
解:(1)有抛物线的定义可知点T(2,t),(t>0)到抛物线的准线的距离为3,
即有2+
=3可得P=2,将T(2,t)代入y2=4x
得t=2
.
(2)∵F(1,0),故设直线AB的方程为:x=my+1(m<0),
联立抛物线方程y2=4x,消元可得:y2-4my-4=0,
令A(x1,y1),B(x2,y2),
则由抛物线的定义可得|AB|=|AF|+|BF|=x1+x2+2=m(y1+y2)+4=4m•m+4=4(m2+1).
∵CD⊥AB,∴CD直线的方程为:x=-
y+1,
同理|CD|=4[(-
)2+1]
从而S四边形ABCD=
|AB||CD|=
•16•(m2+1)(
+1)
=8(2+m2+
)≥8(2+2
)
=32.(当m=-1时取等号).
因此四边形ABCD的面积的最小值为32,此时直线AB的斜率为-1.
即有2+
| p |
| 2 |
得t=2
| 2 |
(2)∵F(1,0),故设直线AB的方程为:x=my+1(m<0),
联立抛物线方程y2=4x,消元可得:y2-4my-4=0,
令A(x1,y1),B(x2,y2),
则由抛物线的定义可得|AB|=|AF|+|BF|=x1+x2+2=m(y1+y2)+4=4m•m+4=4(m2+1).
∵CD⊥AB,∴CD直线的方程为:x=-
| 1 |
| m |
同理|CD|=4[(-
| 1 |
| m |
从而S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| m2 |
=8(2+m2+
| 1 |
| m2 |
m2•
|
=32.(当m=-1时取等号).
因此四边形ABCD的面积的最小值为32,此时直线AB的斜率为-1.
点评:本题主要考查了抛物线方程的求法,抛物线的定义域的应用,直线与抛物线的位置关系,弦长公式的应用,四边形面积的求法以及基本不等式的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中,M,N分别C1D1,BC是的中点,则下列判断正确的是( )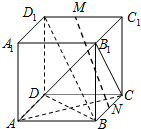

| A、MN∥BD1 |
| B、MN⊥AB1 |
| C、MN∥平面BDD1 |
| D、MN⊥平面AB1C |
甲、乙、丙3位教师安排在周一至周五中的3天值班,要求每人值班1天且每天至多安排1人,则恰好甲安排在另外两位教师前面值班的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|