题目内容
已知函数y=x2-bx+2（x∈（-∞，1））是单调函数，则b的取值范围是 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：二次函数图象是抛物线，开口向上，对称轴是x=
，又y=x2-bx+2（x∈（-∞，1））是单调函数，进而构造关于b的不等式，解不等式可得b的取值范围．
| b |
| 2 |
解答：
解：∵函数y=x2-bx+2的对称轴是x=
，
又∵函数y=x2-bx+2，（x∈（-∞，1））是单调函数，
又∵函数图象开口向上，
∴函数y=x2-bx+2（x∈（-∞，1））是单调减函数，
∴1≤
，
∴b≥2，
∴b的取值范围是[2，+∞）．
故答案为：[2，+∞）．
| b |
| 2 |
又∵函数y=x2-bx+2，（x∈（-∞，1））是单调函数，
又∵函数图象开口向上，
∴函数y=x2-bx+2（x∈（-∞，1））是单调减函数，
∴1≤
| b |
| 2 |
∴b≥2，
∴b的取值范围是[2，+∞）．
故答案为：[2，+∞）．
点评：本题考查二次函数的图象特征、二次函数的单调性及单调区间，体现数形结合的数学思想．
练习册系列答案
相关题目
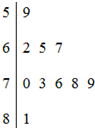已知某山区小学有100名四年级学生，将全体四年级学生随机按00～99编号，并且按编号顺序平均分成10组．现要从中抽取10名学生，各组内抽取的编号按依次增加10进行系统抽样．
执行如图所示的程序框图，若输入如下四个函数：①f（x）=sinx，②f（x）=cosx，③f（x）=
| 1 |
| x |
则输出的函数是（ ）
| A、f（x）=sinx | ||
| B、f（x）=cosx | ||
C、f（x）=
| ||
| D、f（x）=x2 |