题目内容
当a，b∈R时，下列四个命题：
①若a＞b，则a2＞b2；
②若|a|＞b，则a2＞b2；
③若a＞|b|，则a2＞b2；
④若a≠|b|，则a2≠b2．
其中正确的个数是（ ）
①若a＞b，则a2＞b2；
②若|a|＞b，则a2＞b2；
③若a＞|b|，则a2＞b2；
④若a≠|b|，则a2≠b2．
其中正确的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：命题的真假判断与应用
专题：综合题,简易逻辑
分析：通过举反例说明命题①②④错误；
命题③符合不等式的可乘积性，正确．
命题③符合不等式的可乘积性，正确．
解答：
解：对于①，2＞-3，但22＜（-3）2，命题①错误；
对于②，|-2|＞-3，但（-2）2＜（-3）2，命题②错误；
对于③，由a＞|b|，知a＞0，由不等式的可乘积性知，a2＞b2，命题③正确；
对于④，-2≠|2|，但（-2）2=22，命题④错误．
∴正确的命题只有1个．
故选：B．
对于②，|-2|＞-3，但（-2）2＜（-3）2，命题②错误；
对于③，由a＞|b|，知a＞0，由不等式的可乘积性知，a2＞b2，命题③正确；
对于④，-2≠|2|，但（-2）2=22，命题④错误．
∴正确的命题只有1个．
故选：B．
点评：本题考查了命题的真假判断与应用，考查了不等式的性质，训练了举反例法说明一个命题是错误的，是中档题．
练习册系列答案
相关题目
执行如图所示的程序框图，若输入如下四个函数：①f（x）=sinx，②f（x）=cosx，③f（x）=
| 1 |
| x |
则输出的函数是（ ）
| A、f（x）=sinx | ||
| B、f（x）=cosx | ||
C、f（x）=
| ||
| D、f（x）=x2 |
已知集合M={1，2，3}，N={1，2，3，4}．定义映射f：M→N，则从中任取一个映射满足由点A（1，f（1）），B（2，f（2）），C（3，f（3））构成△ABC且AB=BC的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在正方体ABCD-A1B1C1D1中，M，N分别C1D1，BC是的中点，则下列判断正确的是（ ）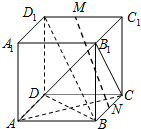
| A、MN∥BD1 |
| B、MN⊥AB1 |
| C、MN∥平面BDD1 |
| D、MN⊥平面AB1C |
若x、y满足约束条件
，则z=x+2y的取值范围是（ ）
|
| A、[0，4] |
| B、[4，6] |
| C、[2，4] |
| D、[2，6] |