题目内容
已知函数f(x)=x3-2x2-4x-7,其导函数为f′(x).
①f(x)的单调减区间是(
,2);
②f(x)的极小值是-15;
③当a>2时,对任意的x>2且x≠a,恒有f(x)>f(a)+f′(a)(x-a);
④函数f(x)有且只有一个零点.
其中真命题的个数为( )
①f(x)的单调减区间是(
| 2 |
| 3 |
②f(x)的极小值是-15;
③当a>2时,对任意的x>2且x≠a,恒有f(x)>f(a)+f′(a)(x-a);
④函数f(x)有且只有一个零点.
其中真命题的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:导数的运算,利用导数研究函数的单调性
专题:导数的概念及应用
分析:由f(x)=x3-2x2-4x-7,知f′(x)=3x2-4x-4,令f′(x)=3x2-4x-4=0,得x=-
,x2=2,分别求出函数的极大值和极小值,知①错误,②④正确;由a>2,x>2且x≠a,利用作差法知f(x)-f(a)-f′(a)(x-a)>0,故③正确;
| 2 |
| 3 |
解答:
解:f(x)=x3-2x2-4x-7,其导函数为f′(x)=3x2-4x-4.
令f′(x)=0,解得x=-
,x=2,
当f′(x)>0时,即x<-
,或x>2时,函数单调递增,
当f′(x)<0时,即-
<x<2时,函数单调递减;
故当x=2时,函数有极小值,极小值为f(-2)=-15,当x=-
时,函数有极大值,极大值为f(-
)<0,
故函数只有一个零点,
①错误,②④正确;∵a>2,x>2且x≠a,
∴f(x)-f(a)-f′(a)(x-a)
=x3-2x2-4x-a3+2a2+4a-(3a2-4a-4)(x-a)
=x3+2a3-2x2-2a2-3a2x+4ax>0,
∴恒有f(x)>f(a)+f′(a)(x-a),
故③正确;
所以中真命题的个数为3个,
故选:C
令f′(x)=0,解得x=-
| 2 |
| 3 |
当f′(x)>0时,即x<-
| 2 |
| 3 |
当f′(x)<0时,即-
| 2 |
| 3 |
故当x=2时,函数有极小值,极小值为f(-2)=-15,当x=-
| 2 |
| 3 |
| 2 |
| 3 |
故函数只有一个零点,
①错误,②④正确;∵a>2,x>2且x≠a,
∴f(x)-f(a)-f′(a)(x-a)
=x3-2x2-4x-a3+2a2+4a-(3a2-4a-4)(x-a)
=x3+2a3-2x2-2a2-3a2x+4ax>0,
∴恒有f(x)>f(a)+f′(a)(x-a),
故③正确;
所以中真命题的个数为3个,
故选:C
点评:本题考查函数的单调区间、极值的求法,以及不等式的应用,解题时要认真审题,仔细解答,注意等价转化思想和导数性质的灵活运用.

练习册系列答案
相关题目
 如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC 上的高,则
如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC 上的高,则| AD |
| AC |
| A、2 | B、4 | C、6 | D、8 |
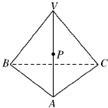 一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )
一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
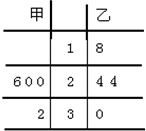 甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示:
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示: