题目内容
经过点M(2,1)作直线l交于双曲线x2-
=1于A,B两点,且M为AB的中点,则直线l的方程为 .
| y2 |
| 2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先,设点A(x1,y1),点B(x2,y2),M(x0,y0),得到2x12-y12=2 ①,2x22-y22=2 ②然后,①-②并结合有关中点坐标公式求解.
解答:
解:设点A(x1,y1),点B(x2,y2),M(x0,y0),
则2x12-y12=2 ①
2x22-y22=2 ②
①-②得
2(x1+x2)(x1-x2)-(y1+y2)(y1-y2)=0,
2×2x0-2y0
=0,
∴8-2k=0,
∴k=4,
∴y-1=4(x-4),
∴直线l的方程为4x-y-15=0,
故答案为:4x-y-15=0.
则2x12-y12=2 ①
2x22-y22=2 ②
①-②得
2(x1+x2)(x1-x2)-(y1+y2)(y1-y2)=0,
2×2x0-2y0
| y1-y2 |
| x1-x2 |
∴8-2k=0,
∴k=4,
∴y-1=4(x-4),
∴直线l的方程为4x-y-15=0,
故答案为:4x-y-15=0.
点评:本题重点考查了直线与双曲线的位置关系、中点弦问题等知识,处理中点弦问题时,常常采用“点差法”进行处理.

练习册系列答案
相关题目
 如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC 上的高,则
如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC 上的高,则| AD |
| AC |
| A、2 | B、4 | C、6 | D、8 |
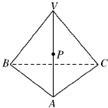 一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )
一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
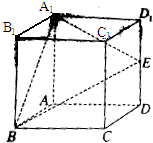 如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正弦值构成的集合是 ( )
如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正弦值构成的集合是 ( )| A、{2} | ||||||||
B、
| ||||||||
C、{t|
| ||||||||
D、{t|
|