题目内容
已知sin（
+α）=
，则cos2α等于（ ）
| π |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点：二倍角的余弦
专题：计算题,三角函数的求值
分析：由sin（
+α）=
及诱导公式可得cosα=
，由二倍角的余弦公式可得cos2α的值．
| π |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
解答：
解：∵sin（
+α）=
，
∴cosα=
，
∴cos2α=2cos2α-1=2×
-1=-
，
故选：C．
| π |
| 2 |
| 1 |
| 3 |
∴cosα=
| 1 |
| 3 |
∴cos2α=2cos2α-1=2×
| 1 |
| 9 |
| 7 |
| 9 |
故选：C．
点评：本题主要考查了二倍角的余弦公式，诱导公式的应用，属于基础题．
练习册系列答案
相关题目
现有五种不同的颜色要对如图形中的四个部分进行着色，要求有公共边的两块不能用同一种颜色，不同的着色方法有化简cos（45°-α）cos（α+15°）-sin（45°-α）sin（α+15°）的结果是（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
如果扇形圆心角的弧度数为2，圆心角所对的弦长也为2，那么这个扇形的面积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设奇函数f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式x[f（x）-f（-x）]＜0的解集为（ ）
| A、（-1，0）∪（1，+∞） |
| B、（-1，0）∪（0，1） |
| C、（-∞，-1）∪（0，1） |
| D、（-∞，-1）∪（1，+∞） |
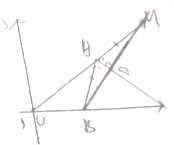如图，△ABC的周长为8，C（0，0），B（2，0），过B的直线与∠CAB的外角平分线垂直，且交AC的延长线于M，求点M的轨迹方程．