题目内容
若圆(x-1)2+(y-2)2=1关于直线y=x+b对称,则实数b= .
考点:圆的标准方程
专题:计算题,直线与圆
分析:由圆(x-1)2+(y-2)2=1关于直线y=x+b对称,知圆心(1,2)在直线y=x+b上,即可求出b的值.
解答:
解:∵圆(x-1)2+(y-2)2=1关于直线y=x+b对称,
∴圆心(1,2)在直线y=x+b上,
∴2=1+b,
解得b=1.
故答案为:1.
∴圆心(1,2)在直线y=x+b上,
∴2=1+b,
解得b=1.
故答案为:1.
点评:本题考查关于直线对称的圆的方程,解题时要认真审题,解题的关键是由圆(x-1)2+(y-2)2=1关于直线y=x+b对称,知圆心(1,2)在直线y=x+b上.

练习册系列答案
相关题目
甲、乙、丙三人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是( )
| A、258 | B、306 |
| C、336 | D、296 |
若两条平行线l1,l2的方程分别是2x+3my-m+2=0,mx+6y-4=0,记l1,l2之间的距离为d,则m,d分别为( )
A、m=2,d=
| ||||
B、m=2,d=
| ||||
C、m=2,d=
| ||||
D、m=-2,d=
|
已知sin(
+α)=
,则cos2α等于( )
| π |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
经过棱锥的高的两个三等分点作两个平行于棱锥底面的截面,则这个棱锥被这两个截面分成的三部分的体积比为( )
| A、1:2:3 |
| B、4:9:27 |
| C、1:8:27 |
| D、1:7:19 |
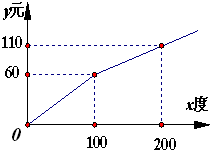 某地的水电资源丰富,并且得到了较好的开发,电力充足.某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的关系如图所示.
某地的水电资源丰富,并且得到了较好的开发,电力充足.某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的关系如图所示.