题目内容
15．已知三棱锥的四个面中，最多共有（ ）个直角三角形？| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 一个三棱锥V-ABC中，侧棱VA⊥底面ABC，并且△ABC中∠B是直角，则可知三棱锥四个面都是直角三角形，从而可得结论
解答 解：如果一个三棱锥V-ABC中，侧棱VA⊥底面ABC，并且△ABC中∠B是直角．
因为BC垂直于VA的射影AB，所以VA垂直于平面ABC的斜线VB，
所以∠VBC是直角．
由VA⊥底面ABC，所以∠VAB，∠VAC都是直角．
因此三棱锥的四个面中∠ABC；∠VAB；∠VAC；∠VBC都是直角．
所以三棱锥最多四个面都是直角三角形．
故选：A
点评 本题重点考查线面垂直的判定与性质，考查学生的探究能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
5．
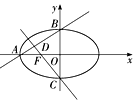如图所示，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，左焦点为F，A、B、C为其三个顶点，直线CF与AB交于D点，则tan∠ADF的值等于（ ）
如图所示，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，左焦点为F，A、B、C为其三个顶点，直线CF与AB交于D点，则tan∠ADF的值等于（ ）| A． | 3$\sqrt{3}$ | B． | -3$\sqrt{3}$ | C． | $\frac{\sqrt{3}}{5}$ | D． | -$\frac{\sqrt{3}}{5}$ |
6．
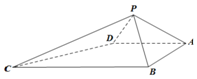如图，四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB和△PAD都是等边三角形，则直线PC与平面ABCD所成角的正切值为（ ）
如图，四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB和△PAD都是等边三角形，则直线PC与平面ABCD所成角的正切值为（ ）| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\sqrt{5}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\sqrt{2}$ |
3．已知中心在原点的椭圆与双曲线有公共焦点，左，右焦点分别为F1，F2，且两条曲线在第一象限的交点为P，△PF1F2是以PF1为底边的等腰三角形，若|PF1|=8，椭圆与双曲线的离心率分别为e1，e2，则e1•e2+1的取值范围是（ ）
| A． | （1，+∞） | B． | $（\frac{8}{3}，+∞）$ | C． | $（\frac{4}{3}，+∞）$ | D． | $（\frac{10}{9}，+∞）$ |
4．已知点A是抛物线$y=\frac{1}{4}{x^2}$的对称轴与准线的交点，点F为该抛物线的焦点，点P在抛物线上，且满足|PF|=m|PA|，当M取得最小值时，点P恰好在以A，F为焦点的双曲线上，则该双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{5}+1}}{2}$ | B． | $\frac{{\sqrt{2}+1}}{2}$ | C． | $\sqrt{2}+1$ | D． | $\sqrt{5}+1$ |
19．下列各组函数中，表示同一函数的是（ ）
| A． | $y=\sqrt{x^2}$和$y=\root{3}{x^3}$ | B． | y=|1-x|和$y=\sqrt{{{（{x-1}）}^2}}$ | ||
| C． | $y=\frac{{{x^2}-1}}{x-1}$和y=x+1 | D． | y=x0和y=1 |