题目内容
6.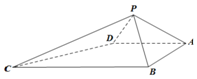 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则直线PC与平面ABCD所成角的正切值为( )
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则直线PC与平面ABCD所成角的正切值为( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
分析 取BD中点O,连结PO,AO,则可证明OP⊥平面ABCD,求出OP,OC即可求解直线PC与平面ABCD所成角的正切值.
解答 证明:取BD中点O,连结PO,AO.
∵△PAB与△PAD都是等边三角形,
∴设AB=AD=PB=PD=PA=1.
∴OP⊥BD,OA⊥BD,
又∠BAD=90°,∴OA=OB=OD=$\frac{\sqrt{2}}{2}$,
∴OP=$\sqrt{P{B}^{2}-O{B}^{2}}$=$\frac{\sqrt{2}}{2}$,
∴OA2+OP2=PA2,∴OP⊥OA.
∴OP⊥平面ABCD,又CO?平面ABCD,
∴OP⊥OC.
OC=$\sqrt{O{B}^{2}+B{C}^{2}-2OB•BCcos∠OBC}$=$\sqrt{({\frac{\sqrt{2}}{2})}^{2}+4-2×\frac{\sqrt{2}}{2}×2×\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{10}}{2}$,
直线PC与平面ABCD所成角的正切值为:tan∠POC=$\frac{PO}{OC}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{10}}{2}}$=$\frac{\sqrt{5}}{5}$.
故选:A.
点评 本题考查直线与平面所成角的求法,考查空间想象能力以及转化思想的应用,计算能力的考查.

练习册系列答案
相关题目
17.已知一个几何体的三视图如图所示,则该几何体的体积是( )
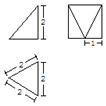

| A. | $2\sqrt{3}$ | B. | $\frac{2}{3}\sqrt{3}$ | C. | $\frac{4}{3}\sqrt{3}$ | D. | $4\sqrt{3}$ |
11.过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则弦AB的长为( )
| A. | 10 | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | $\frac{13}{2}$ |
18.下列函数一定是指数函数的是( )
| A. | y=2x+1 | B. | y=x3 | C. | y=3•2x | D. | y=3-x |
15.已知三棱锥的四个面中,最多共有( )个直角三角形?
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
10.已知圆O的半径为2,PA、PB为圆O的两条切线,A、B为切点(A与B不重合),则$\overrightarrow{PA}$$•\overrightarrow{PB}$的最小值为( )
| A. | -12+4$\sqrt{2}$ | B. | -16+4$\sqrt{2}$ | C. | -12+8$\sqrt{2}$ | D. | -16+8$\sqrt{2}$ |