题目内容
求函数y=2sin（
x+
），x∈[-2π，2π]的单调区间．
| 1 |
| 2 |
| π |
| 3 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由条件利用正弦函数的增减区间，求得f（x）的增减区间．
解答：
解：令2kπ-
≤
x+
≤2kπ+
，k∈z，求得 4kπ-
≤x≤4kπ+
，
可得增区间为[4kπ-
，4kπ+
]，k∈z．
再结合x∈[-2π，2π]，可得增区间为[-
，
]．
令2kπ+
≤
x+
≤2kπ+
，k∈z，求得4kπ+
≤x≤4kπ+
，
可得增区间为[4kπ+
，4kπ+
]，k∈z．
再结合x∈[-2π，2π]，可得增区间为[
，2π]．
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 3 |
| π |
| 3 |
可得增区间为[4kπ-
| 5π |
| 3 |
| π |
| 3 |
再结合x∈[-2π，2π]，可得增区间为[-
| 5π |
| 3 |
| π |
| 3 |
令2kπ+
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 3 |
| 7π |
| 3 |
可得增区间为[4kπ+
| π |
| 3 |
| 7π |
| 3 |
再结合x∈[-2π，2π]，可得增区间为[
| π |
| 3 |
点评：本题主要考查正弦函数的单调性，属于基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图是函数f（x）=x3+ax2+bx+c的大致图象，则|x1-x2|=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知p：（x-1）（x-2）≤0，q：log2（x+1）≤2，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知点A（2，-1），B（4，2），点P在x轴上，当
•
取最小值时，P点的坐标是（ ）
| PA |
| PB |
| A、（2，0） | ||
| B、（4，0） | ||
C、（
| ||
| D、（3，0） |
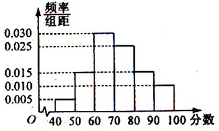我校从高一年级学生中随机抽取部分学生，将他们的数学竞赛成绩分为6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）加以统计，得到如图所示的频率分布直方图．
某学校随机抽取部分新生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中上学所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]，学校规定上学所需时间不小于1小时的学生可以申请在学校住宿．