Question

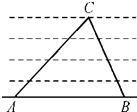如图，为了测定河的宽度，在一岸边选定两点A，B和对岸标记物C，测得∠CAB=30°，∠CBA=45°，AB=120m，则河的宽度为

 

m．

Answer 1

考点：解三角形的实际应用

专题：应用题

分析：过C向AB作垂线，垂足为D，则可中CD即为河的宽度．根据已知∠CAB和∠CBA可用CD分别表示出AD，BD进而相加求得CD，则可的宽度可得．

解答： 解：过C向AB作垂线，垂足为D，CD即为河的宽度．
∵∠CAB=30°，
∴在Rt△ADC中，AD=

3

CD；
在Rt△BCD中，BD=CD，
∴AB=AD+BD=（

3

+1）CD=120，
∴CD=

120

3 +1

=60（

3

-1）m，
答：河的宽度为60（

3

-1）m．
故答案为：60（

3

-1）m．

点评：本题主要考查了解三角形的实际应用．解题的关键是构造出连个直角三角形，在直角三角形中解决问题较为直接．