题目内容
过点P（2，-3）的所有直线中与原点距离最大的直线方程．
考点：点到直线的距离公式
专题：直线与圆
分析：过点P（2，-3）的所有直线中与原点距离最大的直线是与OP垂直的直线，可得要求的直线斜率k=
，利用点斜式即可得出．
| -1 |
| kOP |
解答：
解：过点P（2，-3）的所有直线中与原点距离最大的直线是与OP垂直的直线，
∴要求的直线斜率k=
=
=
．
∴要求的直线方程为：y+3=
（x-2），
化为2x-3y-13=0．
∴要求的直线斜率k=
| -1 |
| kOP |
| -1 | ||
|
| 2 |
| 3 |
∴要求的直线方程为：y+3=
| 2 |
| 3 |
化为2x-3y-13=0．
点评：本题考查了相互垂直的直线斜率之间的关系，属于基础题．
练习册系列答案
相关题目
下列命题中的假命题是（ ）
| A、?x∈R，x2＞0 | ||
B、?x∈R，tanx=
| ||
| C、?x∈R，lnx=0 | ||
| D、?x∈R，3x＞0 |
幂函数y=x-2的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
直线l：2x+3y+6=0的斜率和在y轴上的截距分别为（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
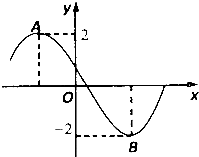如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，