题目内容
在△ABC中，内角A，B，C所对应的边分别为a，b，c，若bsinA-
cosB=0，且b2=ac，则
的值为（ ）
| 3 |
| a+c |
| b |
A、
| ||||
B、
| ||||
| C、2 | ||||
| D、4 |
考点：正弦定理,三角函数中的恒等变换应用,余弦定理
专题：解三角形
分析：先由条件利用正弦定理求得角B，再由余弦定理列出关于a，c的关系式，然后进行合理的变形，求得
的值．
| a+c |
| b |
解答：
解：△ABC中，由bsinA-
cosB=0利用正弦定理得sinBsinA-
sinAcosB=0，∴tanB=
，故B=
．
由余弦定理得b2=a2+c2-2ac•cosB=a2+c2-ac，即 b2=（a+c）2-3ac，
又b2=ac，所以 4b2=（a+c）2，求得
=2，
故选：C．
| 3 |
| 3 |
| 3 |
| π |
| 3 |
由余弦定理得b2=a2+c2-2ac•cosB=a2+c2-ac，即 b2=（a+c）2-3ac，
又b2=ac，所以 4b2=（a+c）2，求得
| a+c |
| b |
故选：C．
点评：本题考查正弦定理、余弦定理得应用．解题先由正弦定理求得角B，再由余弦定理列出关于a，c的关系式，然后进行合理的变形，求得
的值，属于中档题．
| a+c |
| b |
练习册系列答案
阅读快车系列答案
相关题目
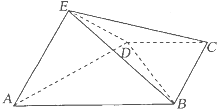如图，在四棱锥E-ABCD中，平面EAD⊥平面ABCD，DC∥AB，BC⊥CD，EA⊥ED，AB=4，BC=CD=EA=ED=2，F是线段EB的中点．实数x、y满足x2+2xy+y2+4x2y2=4，则x-y的最大值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、2
|