题目内容
已知f(x)=x2+2ax+3ln(2x+1)在(0,+∞)上是增函数,则实数a的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:求解f′(x)=2x+2a+
,x>0.利用基本不等式,)(2x+1)+
≥2
(2x+1=
等号成立,即x=
-
)求解出f′(x)=(2x+1)+
+2a-1≥2
+2a-1,据单调性与导数的关系得出2
+2a-1≥0即可.
| 6 |
| 2x+1 |
| 6 |
| 2x+1 |
| 6 |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 6 |
| 2x+1 |
| 6 |
| 6 |
解答:
解:∵f(x)=x2+2ax+3ln(2x+1)
∴f′(x)=2x+2a+
,x>0.
即f′(x)=(2x+1)+
+2a-1,
∵x>0,2x+1>1,(2x+1)+
≥2
(2x+1=
,即x=
-
时等号成立)
∴f′(x)=(2x+1)+
+2a-1≥2
+2a-1,
∵在x∈(0,+∞)上是增函数,
∴只需满足2
+2a-1≥0,即a≥
-
.
∴f′(x)=2x+2a+
| 6 |
| 2x+1 |
即f′(x)=(2x+1)+
| 6 |
| 2x+1 |
∵x>0,2x+1>1,(2x+1)+
| 6 |
| 2x+1 |
| 6 |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
∴f′(x)=(2x+1)+
| 6 |
| 2x+1 |
| 6 |
∵在x∈(0,+∞)上是增函数,
∴只需满足2
| 6 |
| 1 |
| 2 |
| 6 |
点评:本题考查了利用导数研究函数单调性的规律,结合结合基本不等式求解,属于中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
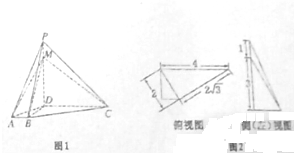 如图1,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,M为侧棱PD上一点,且该四棱锥的俯视图和侧(左)是图如图2所示.
如图1,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,M为侧棱PD上一点,且该四棱锥的俯视图和侧(左)是图如图2所示.(1)证明:BC⊥平面PBD;
(2)证明:AM∥平面PBC.
函数y=x2+x的递增区间是( )
| A、(0,+∞) | ||
| B、(-∞,1) | ||
C、(
| ||
| D、(1,+∞) |
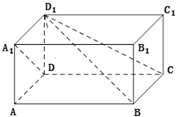 在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,侧棱DD1⊥平面ABCD,且AD=AA1=1,AB=2.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,侧棱DD1⊥平面ABCD,且AD=AA1=1,AB=2.
 如图,正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,那么异面直线BD1与AD所成角的正切值( )
如图,正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,那么异面直线BD1与AD所成角的正切值( )