题目内容

函数y=x2+x的递增区间是（　　）
A、（0，+∞）
B、（-∞，1）
C、（
1
2
，+∞）
D、（1，+∞）
考点：二次函数的性质
专题：函数的性质及应用
分析：先求出函数的对称轴，结合二次函数的性质，从而得到函数的单调区间．
解答： 解：∵函数y=x2+x，对称轴x=
1
2
，
∴函数在（
1
2
，+∞）递增，
故选：C
点评：本题考查了二次函数的性质，考查了函数的单调性，是一道基础题．
练习册系列答案
相关题目
已知函数f（x）=2x2-ax-1，在[-1，2]上单调，则实数a的取值范围是（　　）
A、[-4，8]
B、（-∞，-4]
C、[8，+∞]
D、（-∞，-4]∪[8，+∞）
已知f（x）=x2+2ax+3ln（2x+1）在（0，+∞）上是增函数，则实数a的取值范围是
 
．
定义|
a1a2
a3a4
|=a1a4-a2a3，若函数f（x）=|
2sinx
2
sinx
2
sinxcosx
|，给出下列四个命题：
①f（x）在区间[
π
8
，
5π
8
]上是减函数；
②f（x）关于（
3π
8
，0）中心对称；
③y=f（x）的表达式可改写成y=
2
cos（2x-
π
4
）-1；
④由f（x1）=f（x2）=0可得x1-x2必是π的整数倍；
其中正确命题的序号是
 
．
已知函数f（x）=2asinx•cosx+2cos2x+1，f（
π
6
）=4，
（1）求实数a的值；
（2）求f（x）的单调增区间；
（3）求函数f（x）在x∈[-
π
4
，
π
4
]的值域．
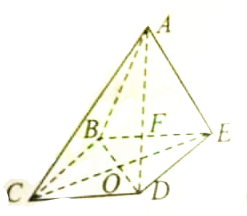如图所示，几何体A-BCDE是底面边长为4的菱形，∠CBE=120°，侧面ABE是等边三角形，BD∩CE=O，F是BE上的动点，面ABE⊥面BCDE；
（1）当F在何处时，OF∥面ABC；
（2）求三棱锥D-ABE的表面积．
函数y=
3+cosx
1-2cosx
的值域是
 
．
已知向量
a
、
b
满足|
a
|=
2
，|
a
-
b
|=
5
，（
a
，
b
）=
π
4
，则|
b
|等于（　　）
A、2
B、
3
C、3
D、2
2
已知曲线C：y=
1
3
x3-2x2+3x+3，
（1）求函数在点（0，3）处的切线方程；
（2）求曲线C在定义域范围的单调区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网