题目内容
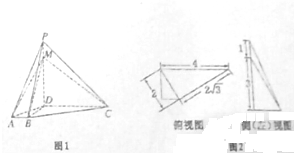 如图1,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,M为侧棱PD上一点,且该四棱锥的俯视图和侧(左)是图如图2所示.
如图1,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,M为侧棱PD上一点,且该四棱锥的俯视图和侧(左)是图如图2所示.(1)证明:BC⊥平面PBD;
(2)证明:AM∥平面PBC.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)利用俯视图和勾股定理的逆定理可得BC⊥BD,利用线面垂直的性质定理可得BC⊥PD,再利用线面垂直的判定定理即可证明;
(2)取PC上一点Q,使PQ:PC=1:4,连接MQ,BQ.利用左视图和平行线分线段成比例的判定和性质即可得出MQ∥CD,MQ=
CD.再利用平行四边形的判定和性质定理即可得出AM∥BQ,利用线面平行的判定定理即可证明.
(2)取PC上一点Q,使PQ:PC=1:4,连接MQ,BQ.利用左视图和平行线分线段成比例的判定和性质即可得出MQ∥CD,MQ=
| 1 |
| 4 |
解答:
证明:(1)由俯视图可得,BD2+BC2=CD2,
∴BC⊥BD.
又∵PD⊥平面ABCD,
∴BC⊥PD,
∵BD∩PD=D,
∴BC⊥平面PBD.
(2)取PC上一点Q,使PQ:PC=1:4,连接MQ,BQ.

由左视图知 PM:PD=1:4,∴MQ∥CD,MQ=
CD
在△BCD中,易得∠CDB=60°,∴∠ADB=30°.
又 BD=2,∴AB=1,AD=
.
又∵AB∥CD,AB=
CD,
∴AB∥MQ,AB=MQ.
∴四边形ABQM为平行四边形,
∴AM∥BQ.
∵AM?平面PBC,BQ?平面PBC,
∴直线AM∥平面PBC.
∴BC⊥BD.
又∵PD⊥平面ABCD,
∴BC⊥PD,
∵BD∩PD=D,
∴BC⊥平面PBD.
(2)取PC上一点Q,使PQ:PC=1:4,连接MQ,BQ.

由左视图知 PM:PD=1:4,∴MQ∥CD,MQ=
| 1 |
| 4 |
在△BCD中,易得∠CDB=60°,∴∠ADB=30°.
又 BD=2,∴AB=1,AD=
| 3 |
又∵AB∥CD,AB=
| 1 |
| 4 |
∴AB∥MQ,AB=MQ.
∴四边形ABQM为平行四边形,
∴AM∥BQ.
∵AM?平面PBC,BQ?平面PBC,
∴直线AM∥平面PBC.
点评:熟练掌握由三视图得到线面位置关系和数据、线面垂直的判定和性质定理、线面平行的判定和性质定理、平行线分线段成比例的判定和性质、平行四边形的判定和性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为测量地面上B,C两点间的距离,在高100m的建筑物顶部选点A,在A出测得点B,C的俯角分别为30°和45°(B,C与建筑物底部在同一水平面上),且∠BAC=45°,则B,C之间的距离为( )
| A、100m | ||
B、100
| ||
C、100
| ||
| D、200m |
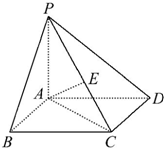 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥AB,PA⊥AC,E是PC的中点,已知AB=2,AD=PA=2,求异面直线BC与AE所成的角的大小.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥AB,PA⊥AC,E是PC的中点,已知AB=2,AD=PA=2,求异面直线BC与AE所成的角的大小.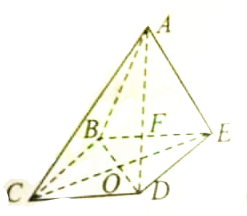 如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;
如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;