题目内容
已知曲线y=f(x)及y=f(x)sinωx,其中f(x)>0,且为可导函数,求证:两曲线在公共点处有相同的切线.
考点:利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:联立两曲线方程,可得sinωx=1,即有cosωx=0,分别求出两函数的导数,判断是否相等,由导数的几何意义,即可得证.
解答:
证明:联立y=f(x)及y=f(x)sinωx,
消去y,可得sinωx=1,
即有cosωx=0,
由于y′=f′(x),
y′=f′(x)sinωx+f(x)ωcosωx=f′(x)sinωx=f′(x),
即有两曲线公共点处的切线的斜率相等,
故两曲线在公共点处有相同的切线.
消去y,可得sinωx=1,
即有cosωx=0,
由于y′=f′(x),
y′=f′(x)sinωx+f(x)ωcosωx=f′(x)sinωx=f′(x),
即有两曲线公共点处的切线的斜率相等,
故两曲线在公共点处有相同的切线.
点评:本题考查导数的几何意义:函数在某点处的导数即为曲线在该点处切线的斜率,正确求导和运用同角的平方关系是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
定义表示不超过x的最大整数[x],记{x}=x-[x],二次函数y=-x2+mx-2与函数y={-x}在(-1,0]上有两个不同的交点,则m的取值范围是( )
A、(-
| ||||
B、(
| ||||
| C、∅ | ||||
| D、以上均不正确 |
长方体ABCD-A1B1C1D1中,AB=BC=
,AA1=
,则异面直线BD1与CC1所成的角等于( )
| 3 |
| 6 |
| A、30° | B、45° |
| C、60° | D、90° |
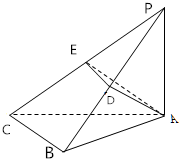 如图,PA⊥平面ABC,AB⊥BC,AD⊥PB,AE⊥PC,AP=
如图,PA⊥平面ABC,AB⊥BC,AD⊥PB,AE⊥PC,AP=