Question

已知大西北某荒漠上A、B两点相距2km，现准备在荒漠上开垦出一片以AB为一条对角线的平行四边形区域建成农艺园，按照规划，围墙总长为8km．
（1）试求四边形另两个顶点的轨迹方程；
（2）问农艺园的最大面积能达到多少？
（3）该荒漠上有一条直线型小溪l刚好通过点A，且l与AB成30°角，现要对整条水沟进行加固改造，但考虑到今后农艺园的水沟要重新设计改造，因此，对水沟可能被农艺园围进的部分暂不加固，则暂不加固的部分有多长？

Answer 1

考点：轨迹方程

专题：圆锥曲线的定义、性质与方程

分析：（1）以AB为x轴、以AB的中垂线直角坐标系，设四边形的顶点C的坐标是（x，y），由题意得|CA|+|CB|=4＞|AB|=2，则动点轨迹为椭圆，由条件求出椭圆方程；
（2）由图和三角形的面积公式求出农艺园的面积S=2S_△ABC=2|y_C|，在由椭圆的范围求出农艺园的最大面积；
（3）将实际问题转化为：直线l与椭圆

x2

4

+

y2

3

=1相交求弦长问题，设P（x₁，y₁），Q（x₂，y₂），再联立直线方程和椭圆方程消去Y后，由根与系数的关系、以及弦长公式进行求解．

解答： 解：（1）以AB为x轴，以AB的中垂线直角坐标系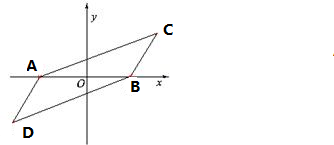，如右图：
设四边形的顶点C的坐标是（x，y），则D（-x，-y）且A（-1，0），B（1，0），
由题意得，|CA|+|CB|=4＞|AB|=2，
所以点C轨迹为椭圆，且a=2，c=1，b=

3

，
四边形另两个顶点的轨迹方程是

x2

4

+

y2

3

=1；
（2）由图得，农艺园的最大面积S=2S_△ABC=2×

1

2

|AB||y_C|=2|y_C|，
因为|y_C|≤

3

，则2|y_C|≤2

3

，
所以农艺园的最大面积能达到2

3

km²；
（3）因为直线型小溪l刚好通过点A，且l与AB成30°角，所以直线l的方程为：y=

3

3

(x+1)，
设直线l与椭圆

x2

4

+

y2

3

=1相交于点P、Q两点，则水沟可能被农艺园围进的部分为PQ，
设设P（x₁，y₁），Q（x₂，y₂），
由

y= 3 3 (x+1) x2 4 + y2 3 =1

得，13x²+8x-32=0，
所以x₁+x₂=-

8

13

，x₁x₂=-

32

13

，
则|PQ|=

(1+ 1 3 )[(x1+x2)2-4x1x2]

=

4 3 [(- 8 13 )2+4× 32 13 ]

=

48

13

（km），
所以暂不加固的部分为

48

13

km．

点评：本题考查圆锥曲线在实际生活中的应用，涉及椭圆的定义、标准方程和性质，直线与圆的位置关系：弦长公式、韦达定理等应用，解题时要认真审题、仔细解答，题目新颖，体现数学与实际生活的关系．