题目内容
在数列{an}中,若a1=1,an+1=an+
,则a101= .
| 1 |
| 2 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:由数列递推式得到数列为等差数列,然后代入等差数列的通项公式求得a101的值.
解答:
解:∵an+1=an+
,
∴an+1-an=
,
则数列{an}构成以
为公差的等差数列,
又a1=1,
∴a101=a1+(101-1)×
=1+100×
=51.
故答案为:51.
| 1 |
| 2 |
∴an+1-an=
| 1 |
| 2 |
则数列{an}构成以
| 1 |
| 2 |
又a1=1,
∴a101=a1+(101-1)×
| 1 |
| 2 |
=1+100×
| 1 |
| 2 |
故答案为:51.
点评:本题考查了数列递推式,考查了等差关系的确定,是中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
函数f(x)的导函数是f′(x),若对任意的x∈R,都有f(x)+2f′(x)<0成立,则( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、无法比较 |
在花园小区内有一块三边长分别为3米、4米、5米的三角形绿化地,有一只小狗在其内部玩耍,若不考虑小狗的大小,则在任意指定的某时刻,小狗与三角形三个顶点的距离均超过1米的概率是( )
A、1-
| ||
B、1-
| ||
C、2-
| ||
D、2-
|
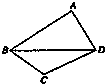 已知一颗粒子的等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在
已知一颗粒子的等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在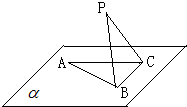 如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=
如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=