题目内容
11.设P(x,y)是曲线C:$\sqrt{\frac{{x}^{2}}{25}}$+$\sqrt{\frac{{y}^{2}}{9}}$=1上的点,F1(-4,0),F2(4,0),则|PF1|+|PF2|的最大值=10.分析 先将曲线方程化简,再根据图形的对称性可知|PF1|+|PF2|的最大值为10.
解答 解:曲线C可化为:$\frac{|x|}{5}+\frac{|y|}{3}$=1,它表示顶点分别为(±5,0),(0,±3)的平行四边形,
根据图形的对称性可知|PF1|+|PF2|的最大值为10,当且仅当点P为(±5,0),(0,±3)时取最大值,
故答案为10.
点评 本题主要考查曲线与方程之间的关系,考查图形的性质,属于基础题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
2.在无穷等比数列{an}中,$\lim_{n→∞}({a_1}+{a_2}+…+{a_n})=\frac{1}{2}$,则a1的取值范围是( )
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})∪$$({\frac{1}{2},1})$ |
19.已知f(x)=sin$\frac{π}{3}$x,A={1,2,3,4,5,6,7,8}现从集合A中任取两个不同元素s、t,则使得f(s)•f(t)=0的可能情况为 ( )
| A. | 12种 | B. | 13种 | C. | 14种 | D. | 15种 |
3.方程4x-4•2x-5=0的解是( )
| A. | x=0或x=log25 | B. | x=-1或x=5 | C. | x=log25 | D. | x=0 |
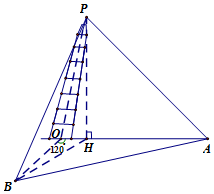 上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求:
上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求: