题目内容
7.若x轴为曲线f(x)=x3-ax-$\frac{1}{4}$的切线,则a=( )| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 求函数的导数,利用导数的几何意义进行求解即可.
解答 解:f(x)=x3-ax-$\frac{1}{4}$,函数的导数f′(x)=3x2-a,
∵x轴为曲线f(x)=x3-ax-$\frac{1}{4}$的切线,
∴f′(x)=0,
设过点为(m,0),
则m3-am-$\frac{1}{4}$=0,①
则f′(m)=3m2-a=0,②
由①②得m=-$\frac{1}{2}$,a=$\frac{3}{4}$,
故选:A.
点评 本题主要考查导数的几何意义,设出切点坐标,求函数的导数,建立方程关系是解决本题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
3.方程4x-4•2x-5=0的解是( )
| A. | x=0或x=log25 | B. | x=-1或x=5 | C. | x=log25 | D. | x=0 |
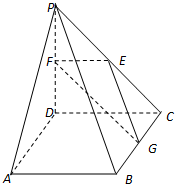 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.